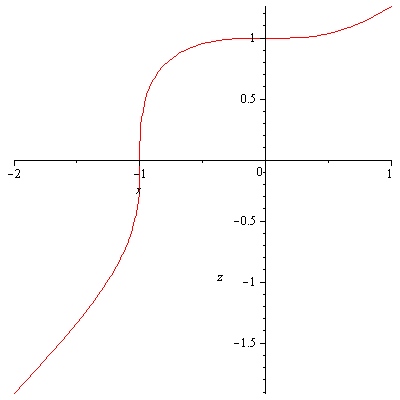Graphs and Partial derivatives: Depicted using Maple
Let us consider f(x,y)=(x^3+y^3)^(1/3).
In Maple type
plot3d(surd(x^3+y^3,3),x=-1..1,y=-1..1);
to obtain (after some rotations):
[The code plot3d((x^3+y^3)^(1/3),x=-1..1,y=-1..1); gives a much less
satisfying result, since Maple interprets t^(1/3) as
e^(ln(t)/3) which has domain t>0.]
Now consider the cross section at y=1. In Maple we now try
plot(surd(x^3+1,3), x = -2 .. 1);
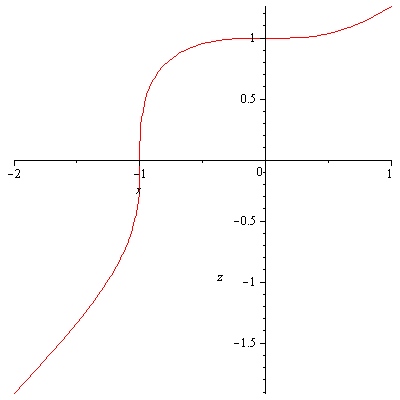
[Again the code plot((x^3+1)^(1/3),x=-2..1); delivers an unsatisfying
result, since Maple only retuns a value for (x^3+1)^(1/3) if
x>-1.]
Notice that this curve is vertical exactly at x=-1, which corresponds
to the fact that the partial derivative f_x(-1,1) does not exist.
Notice that for every other x, f_x(x,1) represents the
slope of the graph z=(x^3+1)^(1/3).
Now let's compute the linear approximation at (0,0):
L_(0,0)(x,y)=f(0,0)+f_x(0,0)(x-0)+f_y(0,0)(y-0)=x+y
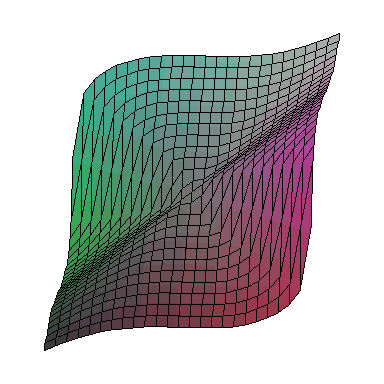
We now graph our function simultaneously with L_(0,0); in Maple
plot3d([surd(x^3+y^3, 3), x+y], x = -1 .. 1, y = -1 .. 1, color = [green, blue])
to obtain (after some rotation):

This doesn't really look like a good approximation to f(x,y), for
(x,y) near (0,0). Verify this by examining the
limit
lim_{(x,y)->(0,0)}|R_{1,(0,0)}(x,y)/||(x,y)-(0,0)||
=lim_{(x,y)->(0,0)}|(x^3+y^3)^{1/3}-x-y|/(x^2+y^2)^{1/2}.
Show that the limit cannot be 0 by testing along the line y=x.
(Moreover, show the limit doesn't even exist.)