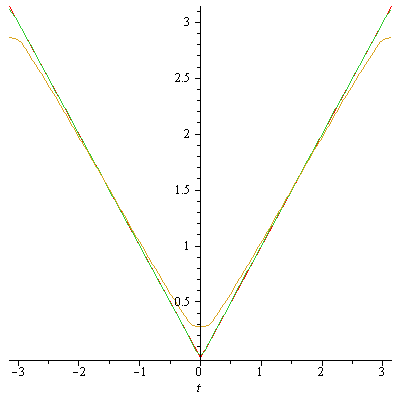Fourier sums vs. Cesaro sums

Lipschitz functions: Fourier sums vs. Cesaro sums

In Maple we define

f := t -> |t|;

The associated Fourier sums are given by

S := proc (n, t) -> (1/2)*Pi-4*(sum(cos((2*j+1)*t)/(2*j+1)^2, j = 0 .. n))/Pi;

and the Cesaro sums are given by

C := proc (n, t) -> (1/2)*Pi-4*(sum((1-(2*j+1)/(n+1))*cos((2*j+1)*t)/(2*j+1)^2, j = 0 .. n))/Pi;

Then, we can plot both simultaneously

n := 10; plot([f(t), S(n, t), C(n, t)], t = -Pi .. Pi);

to obtain (we hope):

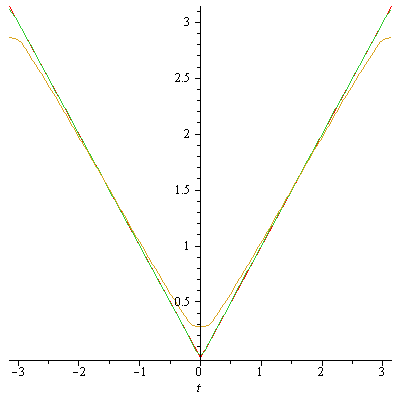
Notice that the green curve (Fourier sums) are approximating f very well, whilst the yellow curve (Cesaro sums) are doind a much worse job. Any explaination?

Let us try this with bigger n, and focus close to 0:

n := 100; plot([f(t), S(n, t), C(n, t)], t = -Pi/n .. Pi/n);

to obtain:

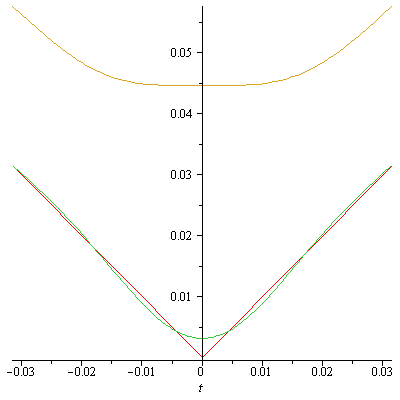
It still looks as if the Fourier sums are bettering the Cesaro sums.