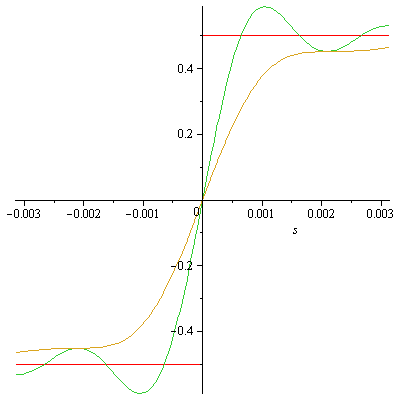Gibbs Phenomenon: Graphed using Maple
In Maple we define
_EnvUseHeavisideAsUnitStep := true:
F:= t -> Heaviside(t)-1/2-t/(2*Pi);
[The annoying _Env... allows Heaviside to be defined at 0.]
The associated Fourier sums are given by
S:= (n,t) -> sum(sin(k*t)/(k*Pi),k=1..n);
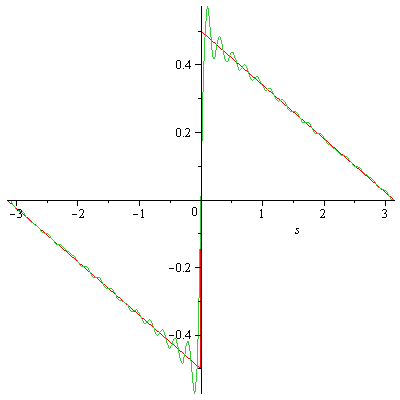
Then, we can plot both simultaneously
n:=30: plot([F(s),S(n,s)],s=-Pi..Pi);
to obtain (we hope):
Note that if we look at the "Gibbs constant" G_s,
evalf(int(sin(x)/(x*Pi),x=0..Pi)-1/2,2) returns
the value 0.09, which is clearly visible as the approximate amount of
"overshoot" for S(30,Pi/30)-F(Pi/30).
Now let's turn our attention to Cesaro sums of the Fourier series.
We have the formula for the Cesaro sum
C:= (n,t) -> sum((1-k/(n+1))sin(k*t)/(k*Pi),k=1..n);
Then, we can plot both simultaneously
n:=30: plot([F(s),S(n,s),C(n,s)],s=-Pi..Pi);
to obtain:
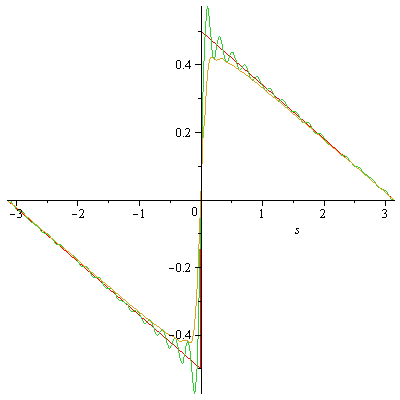
Note that if we look at the secod "Gibbs constant" G_sigma,
evalf(int(sin(x)/(x*Pi),x=0..Pi)-2/Pi^2-1/2,2) returns
the value -0.11. Notice at s=Pi/30 that
C(30,Pi/30)-F(Pi/30) is approximately -0.11. Let us pick a
larger value for n and get a closer view. Try
n:=3000: plot([F(s),S(n,s),C(n,s)],s=-3*Pi/n..3*Pi/n);
to obtain:
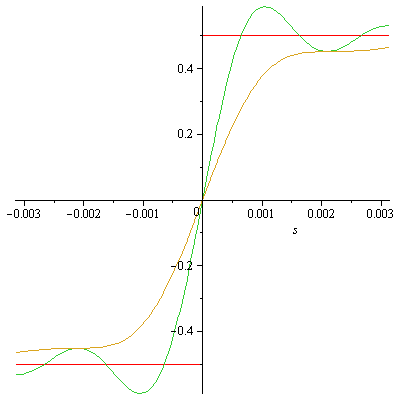
Notice that for s < Pi/3000 (about 0.001),
the Cesaro sum C(3000,s)
is doing a worse job of approximating F(s) than is S(3000,s).
------------------------------------------------------------------------
Let's try, now a square wave:
_EnvUseHeavisideAsUnitStep := true:
F:= t -> Heaviside(t+Pi/2)-Heaviside(t-Pi/2);
which we observe gives the indicator function of the interval [-pi/2,pi/2).
We compute the (2n+1)th Fourier and Ceasaro sums:
S:= (n,t) -> 1/2+2/Pi *sum((-1)^j*cos((2*j+1)*t)/(2*j+1,j=0..n);
C:= (n,t) -> 1/2+2/Pi *sum((1-(2j+1)/(n+1))sin((2*j+1)*t)/(2*j+1),j=0..n);
Then, as before
n:=30: plot([f(t),S(n,t),C(n,t)],t=-Pi..Pi);
to obtain:
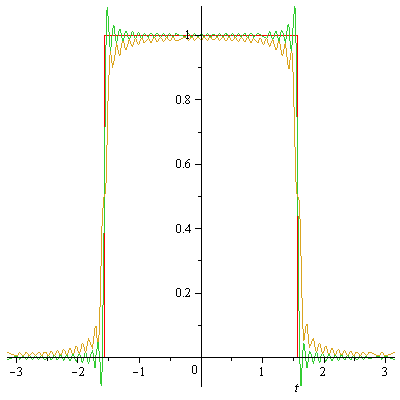
Observe, again, the "Gibbs overshoot" of G_s (approx. 0.09) at the jump
discontinuities. Notice also that C(30,t) seems to generally be a
worse pointwise approximation. Any explaination? (If you think about it,
there is an explianation for why ||f-C(30, . )||_2 is at least as large
as ||f-S(30, . )||_2.) The Gibbs Phenomenon is not merely a curiosity
of Fourier series, but an issue associated with least squares approximations
(Linear Approximation Lemma in Euclidean space). See the very accessible
article
by J. Foster and F. B. Ricahrds which appeared in The American
Mathematical Monthly, v.98, no.1, 1991, pp.47-49.