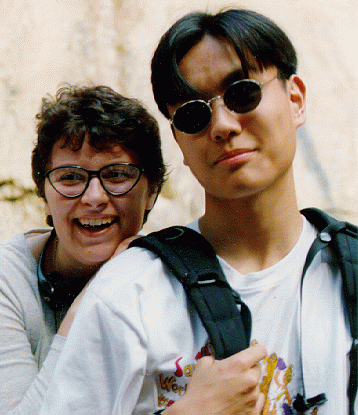
Mihaela Enachescu and Adrian Tang at Johnston Canyon in the Rockies
Photo by Kristin Lord
The road to Taiwan was the culmination of a number of challenging steps for each of these students, and involved a large number of dedicated individuals who gave up much of their time in support of a program that celebrates the best in high school mathematics.
The Winter Training Camp is not the first step to the International Mathematical Olympiad, but it is an important early one. Students are selected on the basis of their performance in a variety of competitions. The 1998 Winter Camp featured a group of 15 students from across the country and a team of trainers and support people: Bill Sands from the University of Calgary, who was there to observe the format of the Winter Camp and to plan for the Summer Camp in Calgary, Dorette Pronk, a Postdoctoral Fellow at Dalhousie, who had agreed to act as Deputy Leader Observer for the Canadian team at the 1998 Olympiad, and my wife Kristin Lord, who was Deputy Leader Observer in Argentina the previous year. There were a couple of "guest" lectures given by David Jackson on combinatorics and by Mary Thompson on extremal problems as well. At the suggestion of some alumni of the Olympiad system, we brought together some older students from previous years, now undergraduates at Waterloo, with our students at the Winter Camp for a closing evening of five-pin bowling. The suggestion of an evening of bowling turned out to be fortuitous, as the freewheeling format, which allowed Richard Hoshino and others to propel bowling balls down the alley in much the same way that Roger Clemens pitches fastballs, was an excellent counterweight to the difficult academic challenges earlier in the camp.
After the Winter Training Camp, the results of competitions such as the Canadian Mathematical Olympiad and the Asia Pacific Mathematical Olympiad were pooled to determine the group of six students who would represent Canada at the International Mathematical Olympiad in Taiwan. The selection committee chose Adrian Birka (Niagara Falls, Ontario), Adrian Chan (Toronto, Ontario), Jimmy Chui (Toronto, Ontario), Mihaela Enachescu (Cote St. Luc, Quebec), Jessie Yin Lei (Windsor, Ontario) and Adrian Tang (Scarborough, Ontario) as its team. It was of some concern that the team concentration was so heavily based in Ontario. However, the selection committee was unanimous in feeling that these were the students whose performance had been of such high caliber as to strongly recommend them for the IMO team. It was also interesting to note that three of our students were named Adrian. We joked about the advantages of having this name in the selection process. Of course, as a statistician I knew that coincidences not only can appear in random selection, but can be expected to appear.
After a week of activities, Georg Gunther had to head home. However, the cavalry rode over the hill in the form of J.P. Grossman, a former gold medal winning IMO constestant and now a doctoral student at M.I.T. J.P. is a top-notch trainer with a wealth of original problems and ideas to share with the students. He was a daily reminder to them that the colour gold was not too high to reach. On July 5, we gathered our belongings in a van rented by Bill Sands and moved from the University of Calgary campus to the beautiful Kananaskis research station in the foothills of the Rocky Mountains. It only took me a few minutes to realise that the Kananaskis site would be excellent for training in mathematics. In a lovely setting with no outside distractions other than the scenery, we were free to work on challenging math problems and go for hikes.
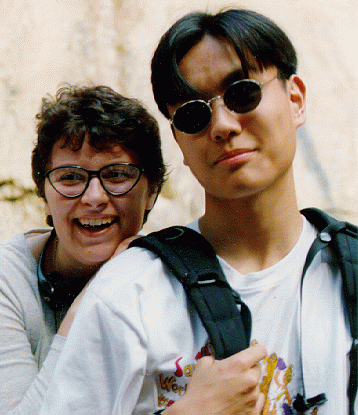
There were a few surprises at this year's IMO. One surprise was an earthquake which shook parts of the island for a few moments while we were there. Sadly, four people in another part of Taiwan died from debris that fell as result of the earthquake. However for the IMO delegates centred in Taipei, the earthquake was only a minor incident at the time it happened. Another surprise that I would not wish to be repeated at a future Olympiad was that many of the students had to sleep on bunk beds with no mattresses. While this is a commonplace practice in Taiwan, many students from North America, Australia and Europe were not accustomed to it.
The 1998 IMO was heavy on number theory and geometry but was reasonably balanced on difficulty. Problem 6 was universally admired by the jury. It asked the contestants to consider all functions f from the set of positive integers to itself such that
for all positive integers s and t. The problem was to determine the least possible value of f(1998).
Each year, medals are handed out at the IMO according to the following rules:
1. No more than 50% of the students should receive medals.
2. Among those receiving medals, the gold, silver and bronze medals are to be awarded as close to the ratio 1:2:3 as possible.
The Canadian team received the following medals:
Jessie Lei was awarded an Honourable Mention, which goes to any student who does not receive a medal but who gets a perfect score on at least one of the problems.
I was delighted with the performance of our team. I also especially pleased by the fact that Mihaela Enachescu was tied with one other woman from the U.S.A. as the highest scoring woman in the competition. Mihaela narrowly missed a gold herself.
The IMO is a competition between individuals, not countries. Therefore students are ranked and honoured in the closing ceremonies of each IMO. Nevertheless, international rivalries being what they are, countries sum the scores of their contestants and compare their summed scores scores with those of other countries. For those who keep track of such things, 1998 was a good year as Canada was ranked 20th out of the 79 countries.
There are many other stories of the 1998 IMO, most of them involving feet for some unexplained reason: the former male team member who showed up one day at the Winter Training Camp wearing high-heeled shoes, the sad story of a cheap frisbee that was artfully and cleverly decorated only to be crushed ignominiously by an awkward teenage limb, and the team member who bravely hiked through Johnston Canyon with bare feet. But perhaps these stories are not mine to tell.
Christopher Small


![[BACK]](home.gif) Back to Christopher Small's home page .
Back to Christopher Small's home page .
![[BACK]](graph.gif) Back to the Statistics and Actuarial Science home page .
Back to the Statistics and Actuarial Science home page .