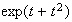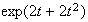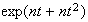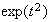-
-
Each student can choose in 4 ways and they each get to choose. So
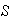 has
has
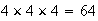 points.
points.
-
The first student can choose in 4 ways and the others then only have 1 section they can go in.
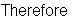
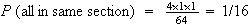 .
.
-
The first to pick has 4 ways to choose, the next has 3 sections left, and the last has 2 sections left.
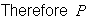 (different sections) =
(different sections) =
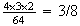 .
.
-
Each has 3 ways to choose a section.
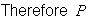 (nobody in section 1) =
(nobody in section 1) =
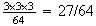
-
-
Now
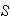 has
has
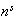 points
points
-
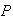 (all in same section) =
(all in same section) =
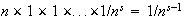
-
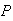 (different sections) =
(different sections) =
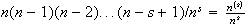 .
.
-
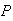 (nobody in section 1) =
(nobody in section 1) =
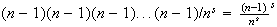
-
-
-
-
There are 26 ways to choose each of the 3 letters, so in all the letters can be chosen in
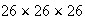 ways. If all letters are the same, there are 26 ways to choose the first
letter, and only 1 way to choose the remaining 2 letters. So
ways. If all letters are the same, there are 26 ways to choose the first
letter, and only 1 way to choose the remaining 2 letters. So
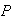 (all letters the same) is
(all letters the same) is
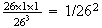 .
.
-
There are
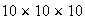 ways to choose the 3 digits. The number of ways to choose all even digits is
ways to choose the 3 digits. The number of ways to choose all even digits is
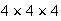 .
The number of ways to choose all odd digits is
.
The number of ways to choose all odd digits is
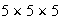 .
.
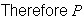 (all even or all odd) =
(all even or all odd) =
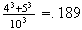 .
.
-
-
-
There are 35 symbols in all (26 letters + 9 numbers). The number of different 6-symbol passwords is
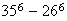 (we need to subtract off the
(we need to subtract off the
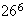 arrangements in which only letters are used, since there must be at least one
number). Similarly, we get the number of 7-symbol and 8-symbol passwords as
arrangements in which only letters are used, since there must be at least one
number). Similarly, we get the number of 7-symbol and 8-symbol passwords as
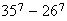 and
and
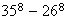 .
The total number of possible passwords is then
.
The total number of possible passwords is then
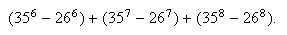
-
Let
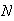 be the answer to part (a) (the total no. of possible passwords). Assuming you
never try the same password twice, the probability you find the correct
password within the first 1,000 tries is
be the answer to part (a) (the total no. of possible passwords). Assuming you
never try the same password twice, the probability you find the correct
password within the first 1,000 tries is
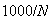 .
.
-
-
There are 7! different orders
-
We can stick the even digits together in 3! orders. This block of even digits plus the 4 odd digits can be arranged in 5! orders.
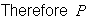 (even together) =
(even together) =
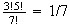
-
For even at ends, there are 3 ways to fill the first place, and 2 ways to fill the last place and 5! ways to arrange the middle 5 digits. For odd at ends there are 4 ways to fill the first place and 3 ways to fill the last place and 5! ways to arrange the middle 5 digits.
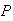 (even or odd ends) =
(even or odd ends) =
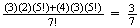 .
.
-
-
The number of arrangements in
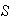 is
is
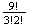
-
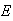 at each end gives
at each end gives
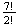 arrangements of the middle 7 letters.
arrangements of the middle 7 letters.
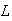 at each end gives
at each end gives
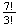 arrangements of the middle 7 letters.
arrangements of the middle 7 letters.
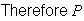 (same letter at ends) =
(same letter at ends) =
-
The
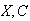 and
and
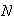 can be ``stuck'' together in
can be ``stuck'' together in
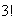 ways to form a single unit. We can then arrange the
ways to form a single unit. We can then arrange the
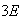 's,
's,
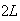 's,
's,
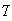 ,
and
,
and
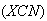 in
in
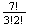 ways.
ways.
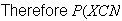 together)
=
together)
=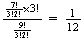 .
.
-
There is only 1 way to arrange the letters in the order CEEELLNTX.
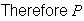 (alphabetical order) =
(alphabetical order) =
-
-
-
The 8 cars can be chosen in
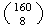 ways. We can choose
ways. We can choose
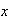 with faulty emission controls and
with faulty emission controls and
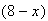 with good ones in
with good ones in
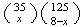 ways.
ways.
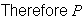 (at least 3 faulty) =
(at least 3 faulty) =
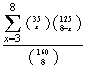 since we need
since we need
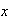 = 3 or 4 or .... or 8.
= 3 or 4 or .... or 8.
-
This assumes all
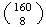 combinations are equally likely. This assumption probably doesn't hold since
the inspector would tend to select older cars or those in bad shape.
combinations are equally likely. This assumption probably doesn't hold since
the inspector would tend to select older cars or those in bad shape.
-
-
-
The first 6 finishes can be chosen in
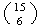 ways. Choose 4 from numbers
ways. Choose 4 from numbers
1,2, ...., 9 in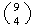 ways and 2 from numbers 10, ..., 15 in
ways and 2 from numbers 10, ..., 15 in
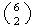 ways.
ways.
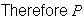 (4 single digits in top 6) =
(4 single digits in top 6) =
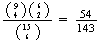 .
.
-
Need 2 single digits and 2 double digit numbers in 1
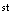 4 and then a single digit. This occurs in
4 and then a single digit. This occurs in
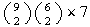 ways.
ways.
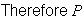 (5
(5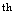 is
is
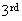 single digit) =
single digit) =
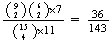 .
(since we can choose
.
(since we can choose
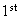 4 in
4 in
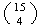 ways and then have 11 choices for the
ways and then have 11 choices for the
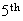 )
)
Alternate Solution: There are
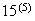 ways to choose the first 5 in order. We can choose in order, 2 double digit
and 3 single digit finishers in
ways to choose the first 5 in order. We can choose in order, 2 double digit
and 3 single digit finishers in
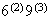 ways, and then choose which 2 of the first 4 places have double digit numbers
in
ways, and then choose which 2 of the first 4 places have double digit numbers
in
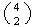 ways.
ways.
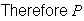 (
(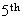 is
is
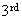 single digit)
=
single digit)
=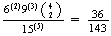 .
.
-
Choose 13 in 1 way and the other 6 numbers in
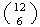 ways. (from 1,2, ....., 12).
ways. (from 1,2, ....., 12).
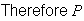 (13 is highest) =
(13 is highest) =
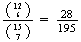 .
.
Alternate Solution: From the
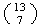 ways to choose 7 numbers from 1,2, ..., 13 subtract the
ways to choose 7 numbers from 1,2, ..., 13 subtract the
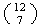 which don't include 13 (i.e. all 7 chosen from 1,2, ..., 12).
which don't include 13 (i.e. all 7 chosen from 1,2, ..., 12).
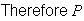 (13 is highest) =
(13 is highest) =
-
-
Let
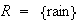 and
and
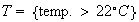 ,
and draw yourself a Venn diagram. Then
,
and draw yourself a Venn diagram. Then
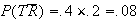
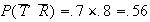
(Note that the information that 40% of days with temp
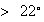 have no rain is not needed to solve the question).
have no rain is not needed to solve the question).
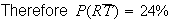
This result is to be expected since 80% of days have a high temperature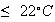 and 30% of these days have rain.
and 30% of these days have rain.
-
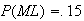
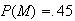
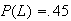 See the Figure
below:
See the Figure
below:
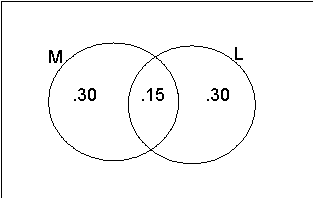
The region outside the circles represents females to the right. To make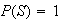 .
we need
.
we need
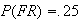 .
.
-
-
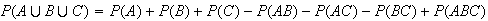
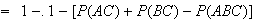
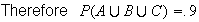 is the largest value, and this occurs when
is the largest value, and this occurs when
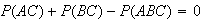 .
.
-
Since
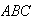 is contained within both
is contained within both
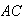 and
and
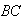 we know
we know
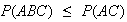 and
and
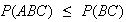 .
Thus
.
Thus
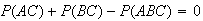 iff
iff
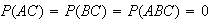 .
.
While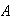 and
and
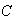 could be mutually exclusive, it can't be determined for sure.
could be mutually exclusive, it can't be determined for sure.
-
-
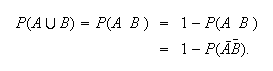 Alternatively, (look at a Venn diagram),
Alternatively, (look at a Venn diagram),
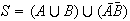 is a partition, so
is a partition, so
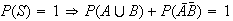 .
.
-
-
Points giving a total of 9 are: (3,6), (4,5), (5,4) and (6,3). The probabilities are (.1)(.3) = .03 for (3,6) and for (6,3), and (.2)(.2) = .04 for (4,5) and for (5,4).
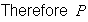 (3, 6) or (4, 5) or (5, 4) or (6, 3)) = .03 + .04 + .04 + .03 = .14.
(3, 6) or (4, 5) or (5, 4) or (6, 3)) = .03 + .04 + .04 + .03 = .14.
-
There are
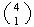 arrangements with 1 nine and 3 non-nines. Each arrangement has probability
arrangements with 1 nine and 3 non-nines. Each arrangement has probability
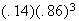 .
.
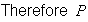 (nine on 1 of 4 repetitions) =
(nine on 1 of 4 repetitions) =
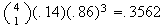
-
-
Let
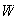 = {at least 1 woman} and
= {at least 1 woman} and
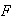 = {at least 1 French speaking
student}.
= {at least 1 French speaking
student}.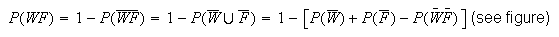
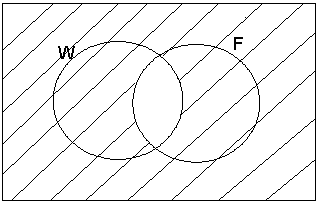
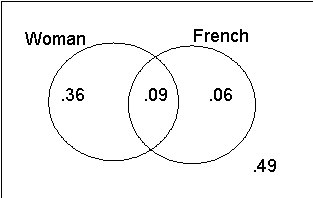
Venn diagram, Problem 4.3.2
But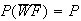 (no woman and no French speaking
student)
(no woman and no French speaking
student)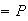 (all men who don't speak
French)
(all men who don't speak
French)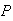 (woman who speaks French)
=
(woman who speaks French)
=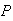 (woman)P(French\woman)=
(woman)P(French\woman)=
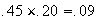 .
.
P(woman who speaks french)
From Venn diagram, (man without French) =
.49.
(man without French) =
.49.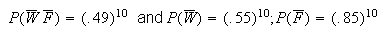
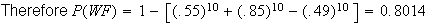 .
.
-
From a Venn diagram: (1)
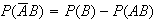 (2)
(2)
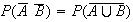
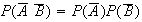
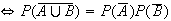
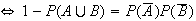
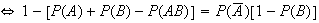
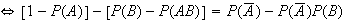
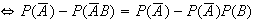
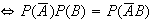
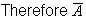 and
and
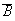 are independent iff
are independent iff
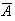 and
and
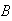 are independent.
are independent.
-
Let
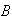 =
=
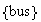 and
and
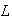 =
=
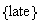 .
.
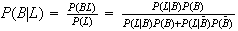
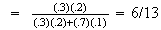
-
Let
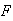 =
=
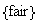 and
and
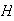 =
=
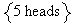
-
Let
 = { defective headlights},
= { defective headlights},
 = {defective muffler}
= {defective muffler}
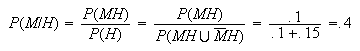
-
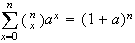
Differentiate with respect to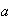 on both
sides:
on both
sides: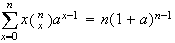 .
Multiply by
.
Multiply by
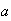 to get
to get
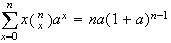
Let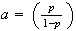 .
Then
.
Then
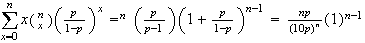
Multiply by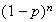 :
: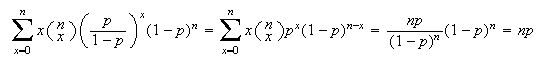
-
Let
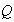 = {heads on quarter} and
= {heads on quarter} and
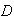 ={heads on dime}. Then
={heads on dime}. Then
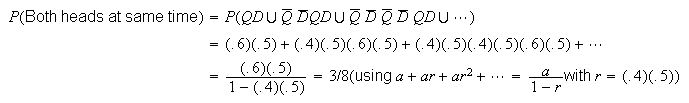
-
We need
 and
and
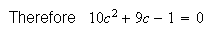
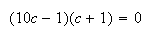
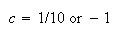 But if
But if
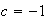 we have
we have
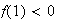 ... impossible.
... impossible.

-
We are arranging
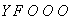 where
where
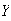 = {you},
= {you},
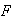 = {friend}, O = {other}. There are
= {friend}, O = {other}. There are
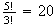 distinct arrangements.
distinct arrangements.
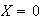 :
: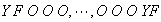 has 4 arrangements with
has 4 arrangements with
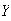 first and 4 with
first and 4 with
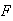 first.
first.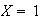 :
: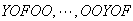 has 3 arrangements with
has 3 arrangements with
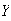 first and 3 with
first and 3 with
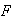 first.
first.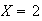 :
: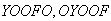 has 2 with
has 2 with
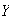 first and 2 with
first and 2 with
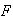 .
.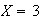 :
: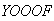 has 1 with
has 1 with
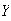 first and 1 with
first and 1 with
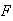 .
.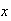
0 1 2 3 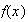
.4 .3 .2 .1 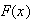
.4 .7 .9 1 -
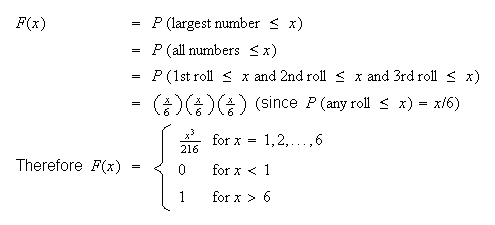
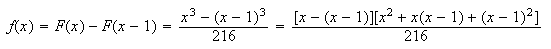
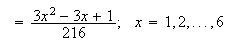
-
-
Using the hypergeometric distribution,
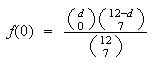
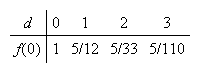
-
While we could find none tainted if
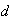 is as big as 3, it is not likely to happen.
is as big as 3, it is not likely to happen.
This implies the box is not likely to have as many as 3 tainted tins.
-
-
Considering order, there are
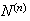 points in
points in
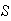 .
We can choose which
.
We can choose which
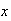 of the
of the
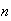 selections will have "success" in
selections will have "success" in
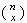 ways. We can arrange the
ways. We can arrange the
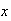 "successes" in their selected positions in
"successes" in their selected positions in
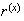 ways and the
ways and the
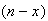 "failures" in the remaining positions in
"failures" in the remaining positions in
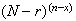 ways.
ways.
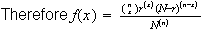 with
with
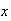 ranging from max
ranging from max
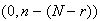 to min
to min
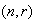
-
-
Using hypergeometric, with
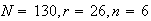 ,
,
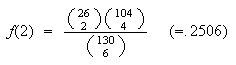
-
Using binomial as an approximation,
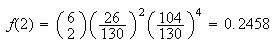
-
-
-
(a)
-
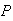 (fail twice)
(fail twice)
=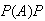 (fail twice
(fail twice
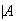 )
+
)
+
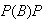 (fail twice
(fail twice
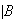 )
)
=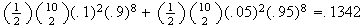 .
.
Where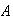 = { camera
= { camera
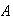 is picked }
is picked }
and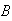 = { camera
= { camera
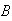 is picked }
is picked }
This assumes shots are independent with a constant failure probability.
-
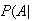 failed twice) =
failed twice) =
-
-
We need
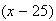 "failures" before our 25th "success".
"failures" before our 25th "success".
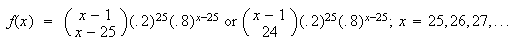
-
-
In the first
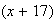 selections we need to get
selections we need to get
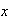 defective (use hypergeometric distribution) and then we need a good one on the
defective (use hypergeometric distribution) and then we need a good one on the
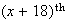 draw.
draw.
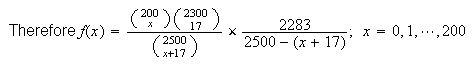
-
Since 2500 is large and we're only choosing a few of them, we can approximate the hypergeometric portion of
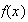 using binomial
using binomial
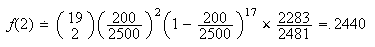
-
-
Using geometric,
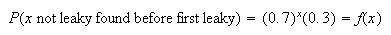
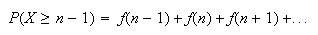
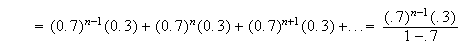
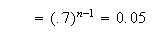
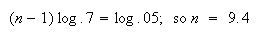 At least 9.4 cars means 10 or more cars must be checked
At least 9.4 cars means 10 or more cars must be checked
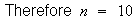
-
-
Let
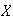 be the number who don't show. Then
be the number who don't show. Then
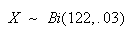
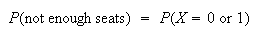
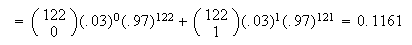 (To use a Poisson approximation we need
(To use a Poisson approximation we need
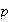 near
near
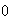 .
That is why we defined "success" as not showing up).
.
That is why we defined "success" as not showing up).
For Poisson,
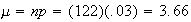
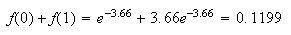
-
Binomial requires all passengers to be independent as to showing up for the flight, and that each passenger has the same probability of showing up. Passengers are not likely independent since people from the same family or company are likely to all show up or all not show. Even strangers arriving on an earlier incoming flight would not miss their flight independently if the flight was delayed. Passengers may all have roughly the same probability of showing up, but even this is suspect. People travelling in different fare categories or in different classes (e.g. charter fares versus first class) may have different probabilities of showing up.
-
-
-
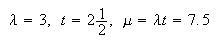
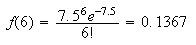
-
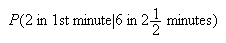
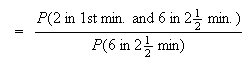
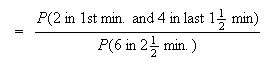
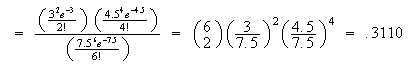 Note this is a binomial probability function.
Note this is a binomial probability function.
-
-
Assuming the conditions for a Poisson process are met, with lines as units of ``time":
-
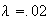 per line;
per line;
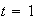 line;
line;
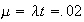
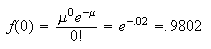
-
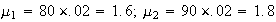
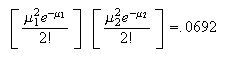
-
-
Consider a 1 minute period with no occurrences as a ``success''. Then
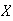 has a geometric distribution. The probability of ``success'' is
has a geometric distribution. The probability of ``success'' is
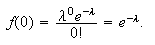
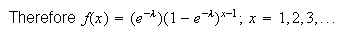 (There must be
(There must be
 failures before the first success.)
failures before the first success.)
-
-
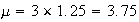
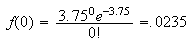
-
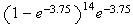 ,
using a geometric distribution
,
using a geometric distribution
-
Using a binomial distribution
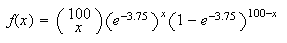 Approximate by Poisson with
Approximate by Poisson with
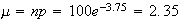
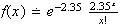 (
(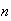 large,
large,
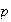 small)
small)
Thus,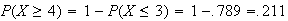 .
.
-
-
There are 10 tickets with all digits identical. For these there is only 1 prize. There are
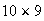 ways to pick a digit to occur twice and a different digit to occur once. These
can be arranged in
ways to pick a digit to occur twice and a different digit to occur once. These
can be arranged in
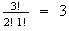 different orders; i.e. there are 270 tickets for which 3 prizes are paid.
There are
different orders; i.e. there are 270 tickets for which 3 prizes are paid.
There are
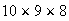 ways to pick 3 different digits in order. For each of these 720 tickets there
will be 3! prizes paid.
ways to pick 3 different digits in order. For each of these 720 tickets there
will be 3! prizes paid.
The organization takes in $1,000.
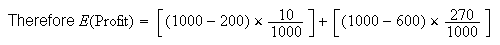
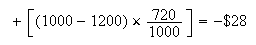 i.e., on average they lose $28.
i.e., on average they lose $28.
-
Let them sell
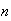 tickets. Suppose
tickets. Suppose
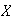 show up. Then
show up. Then
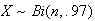 .
For binomial,
.
For binomial,
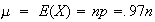
If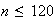 ,
revenues will be
,
revenues will be
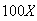 ,
and
,
and
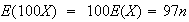 .
This is maximized for
.
This is maximized for
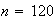 .
.
 Max. expected revenue is $11,640.
Max. expected revenue is $11,640.
For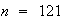 ,
revenues are
,
revenues are
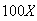 ,
less $500 if all 121 show up.
,
less $500 if all 121 show up.
i.e.,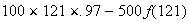
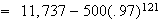 = $11,724.46 is expected.
= $11,724.46 is expected.
For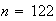 ,
revenues are
,
revenues are
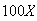 ,
less $500 if 121 show up, less $1000 if all 122 show.
,
less $500 if 121 show up, less $1000 if all 122 show.
i.e.,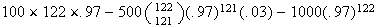
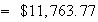 is expected.
is expected.
For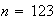 ,
revenues are
,
revenues are
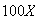 ,
less $500 if 121 show, less $1,000 if 122 show, less $1500 if all 123 show.
,
less $500 if 121 show, less $1,000 if 122 show, less $1500 if all 123 show.
i.e.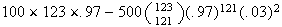
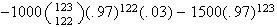
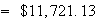 is expected.
is expected.
 They should sell 122 tickets.
They should sell 122 tickets.
-
-
Let
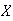 be the number of words needing correction and let
be the number of words needing correction and let
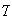 be the time to type the passage. Then
be the time to type the passage. Then
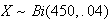 and
and
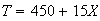 .
.
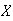 has mean
has mean
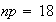 and variance
and variance
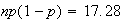 .
.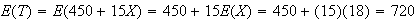
Var =
Var
=
Var Var
Var .
.
-
At 45 words per minute, each word takes
 seconds.
seconds.
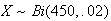 and
and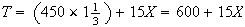
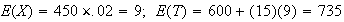 ,
so it takes longer on average.
,
so it takes longer on average.
-
-
-
The marginal probability functions are:
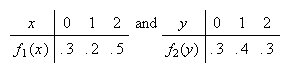
Since
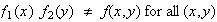
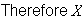 and
and
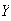 are not independent.
are not independent.
e.g.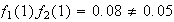
-
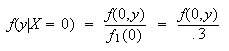
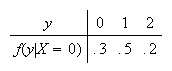
-

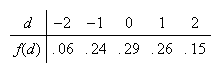
(e.g.
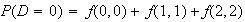 )
)
-
-
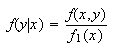
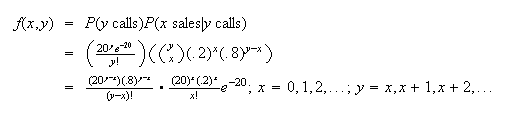 (
(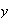 starts at
starts at
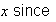 no. of calls
no. of calls
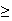 no. of sales).
no. of sales).
-
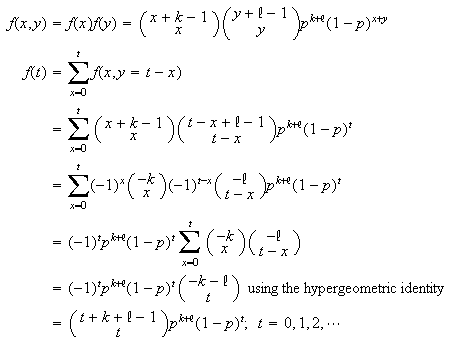 using the given identity on
using the given identity on
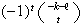 .
(
.
(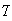 has a negative binomial distribution)
has a negative binomial distribution)
-
-
Use a multinomial distribution.
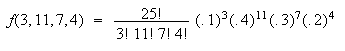
-
Group
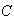 's
and
's
and
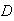 's
into a single category.
's
into a single category.
-
Of the 21 non
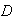 's
we need
's
we need
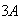 's,
's,
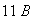 's
and
's
and
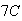 's.
The (conditional) probabilities for the
non-
's.
The (conditional) probabilities for the
non-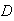 's
are: 1/8 for
's
are: 1/8 for
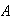 ,
4/8 for
,
4/8 for
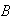 ,
and
,
and
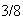 for
for
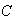 .
.
(e.g.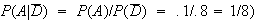
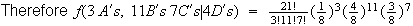 .
.
-
-
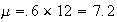
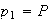 (fewer than 5 chips) =
(fewer than 5 chips) =
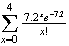
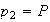 (more than 9 chips) =
(more than 9 chips) =
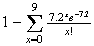
-
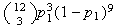
-
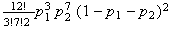
-
Given that 7 have
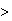 9 chips, the remaining 5 are of 2 types - under 5 chips, or 5 to 9 chips
9 chips, the remaining 5 are of 2 types - under 5 chips, or 5 to 9 chips
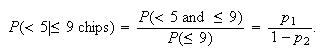 Using a binomial distribution,
Using a binomial distribution,
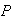 (3 under
5
(3 under
5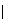 7
over 9) =
7
over 9) =
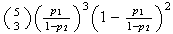
-
-
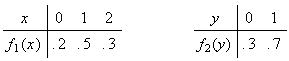
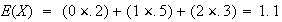
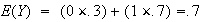
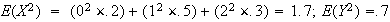
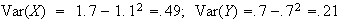
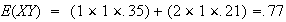
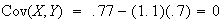
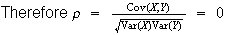
While
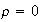 indicates
indicates
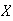 and
and
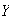 may be independent (and indeed are in this case), it does not prove that they
are independent. It only indicates that there is no linear relationship
between
may be independent (and indeed are in this case), it does not prove that they
are independent. It only indicates that there is no linear relationship
between
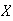 and
and
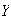 .
.
-
-
-
If
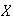 and
and
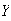 are independent then
Cov
are independent then
Cov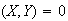 ,
and so
,
and so
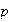 must be 5/72. But if
must be 5/72. But if
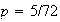 then
then
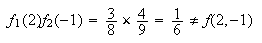
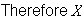 and
and
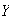 cannot be independent for any value of
cannot be independent for any value of
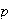
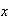
2 4 6 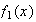
3/8 3/8 1/4 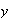
-1 1 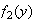
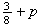
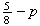
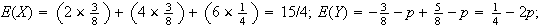
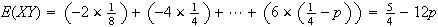
Cov
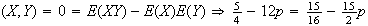
Therefore
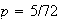
-
-

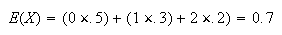
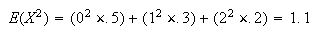
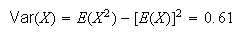
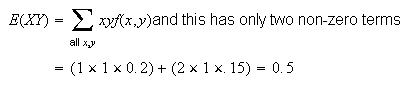
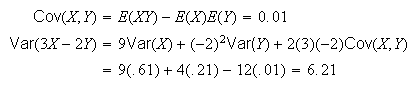
-
Let
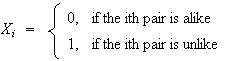
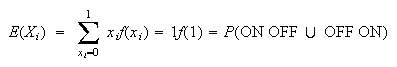
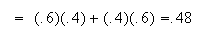
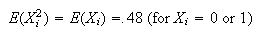
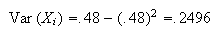 Pairs are independent if they have no common points, but may not be
independent if the pairs are adjacent.
Pairs are independent if they have no common points, but may not be
independent if the pairs are adjacent.
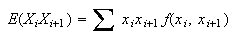
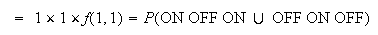
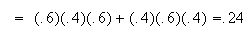
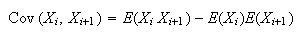
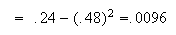
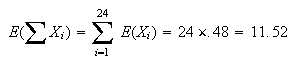
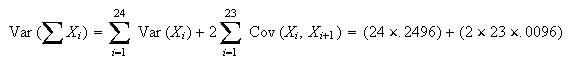
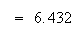
-
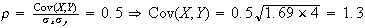
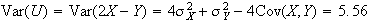
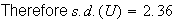
-
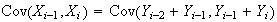
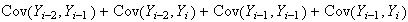
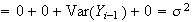
Also,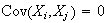 for
for
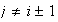 and
and
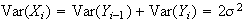
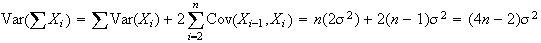
-
Using
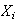 as
defined,
as
defined,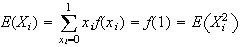 since
since
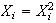
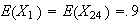 since only 1 cut is
needed
since only 1 cut is
needed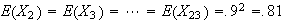 since 2 cuts are
needed.
since 2 cuts are
needed.
Var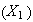 =
Var
=
Var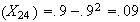
Var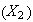 =
Var
=
Var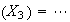 =
Var
=
Var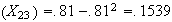
Cov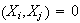 if
if
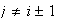 since there are no common pieces and cuts are
independent.
since there are no common pieces and cuts are
independent.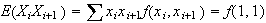
(product is 0 if either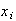 or
or
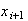 is a
0)
is a
0)
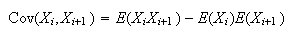
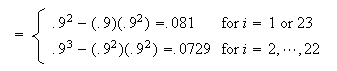
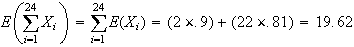
Var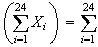 Var
Var
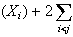 Cov
Cov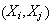
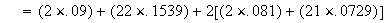
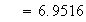
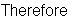 s.d.
s.d.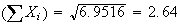
-
-
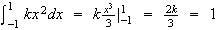
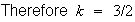
-
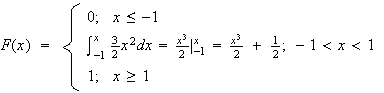
-
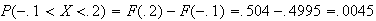
-
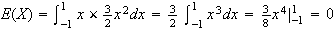 ;
;
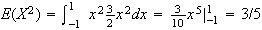
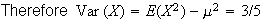
-
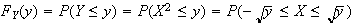
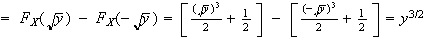
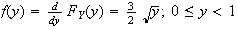
-
-
-
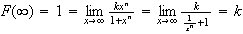
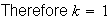
-
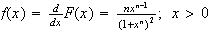
-
Let
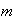 be the median. Then
be the median. Then
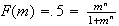
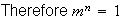 and so the median is 1
and so the median is 1
-
-
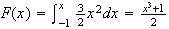 .
.
If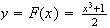 is a random number between
is a random number between
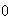 and
and
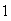 ,
then
,
then
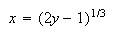 For
For
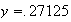 we get
we get
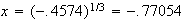
-
Let the time to disruption be
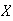 .
.
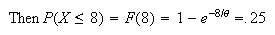
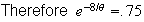 .
Take natural logs.
.
Take natural logs.
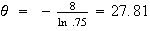 hours.
hours.
-
-
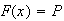 (distance
(distance
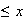 )
=
)
=
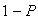 (distance
(distance
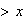 )
)
=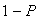 (0 flaws or 1 flaw within radius
(0 flaws or 1 flaw within radius
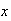 )
)
The number of flaws has a Poisson distribution with mean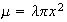
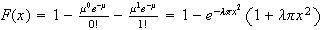
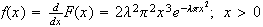
-
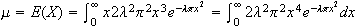
Let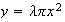 .
Then
.
Then
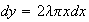 ,
so
,
so
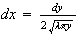
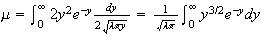
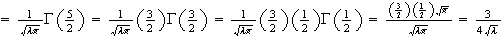
-
-
-
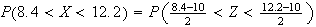 .
.
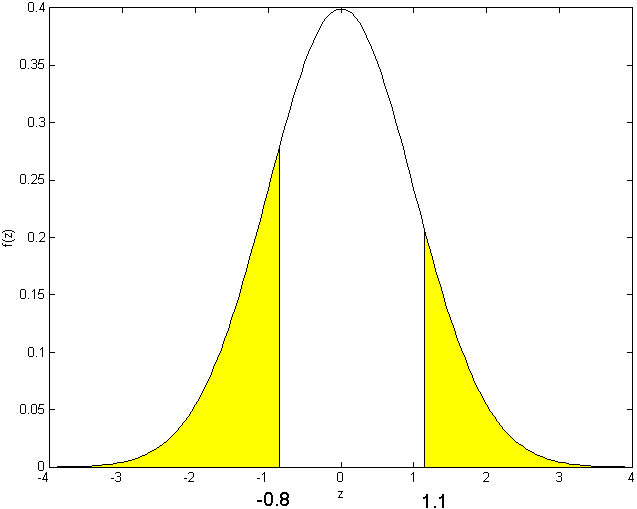
\begin{tabbing} = \=~~ $P ( - .8 < Z < 1.1 )$ \\ = \> $ F (1.1) - F (-.8)$ \\ = \> $F (1.1) - [ 1 - F (.8) ]$ \\ = \> $.8643 - (1 - .7881 ) = .6524$ \end{tabbing} (see the figure)
-
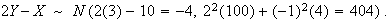
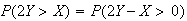
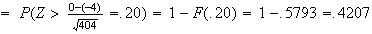
-
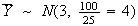
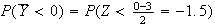
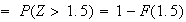
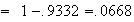 (see the figure)
(see the figure)
-
-
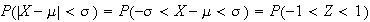
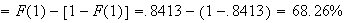 (about 2/3)
(about 2/3)
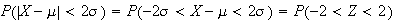
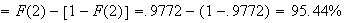 (about 95%)
(about 95%)
Similarly,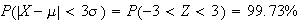 (over 99%)
(over 99%)
-
-
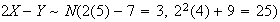
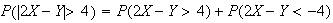
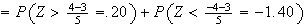
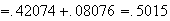
-
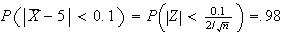
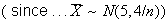
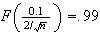
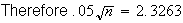
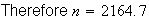 .
Take
.
Take
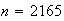 observations.
observations.
-
-
Let
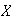 be the number germinating.
be the number germinating.
Then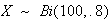 .
.
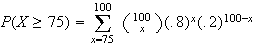 .
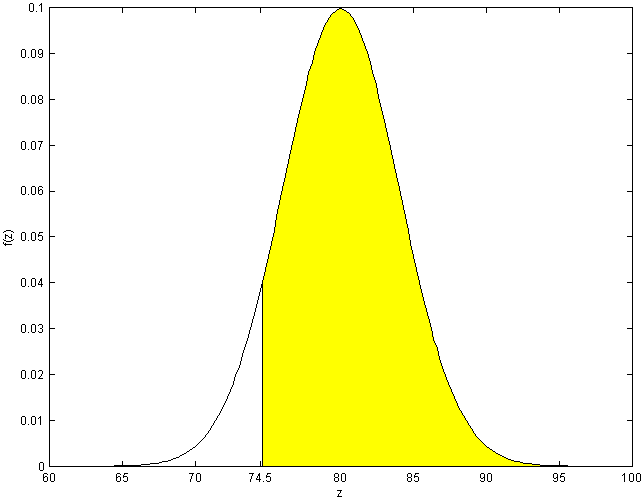
(see the
figure)
.
(see the
figure)
Approximate using a normal distribution with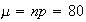 and
and
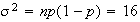 .
.
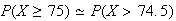
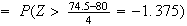
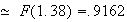
Possible variations on this solution include calculating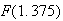 as
as
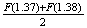 and realizing that
and realizing that
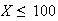 means
means
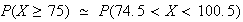 .
However
.
However
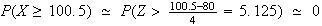 so we get the same answer as before.
so we get the same answer as before.
-
Let
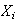 be the cost associated with inspecting part
be the cost associated with inspecting part
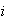
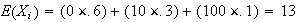
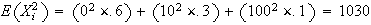
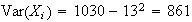
By the central limit theorem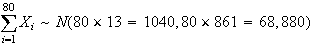 approx.
approx.
Since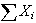 increases in $10
increments,
increases in $10
increments,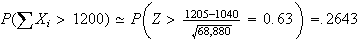
\setcounter{figure}{0}
11. Answers to End of Chapter ProblemsChapter 2:
-
Label the profs
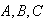 and
and
 .
.
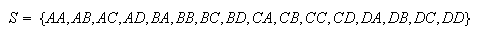
-
1/4
-
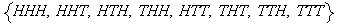
 (b)
(b)
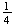 ;
;
-
(1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4), (3,5), (4,5); 0.4;
-
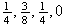
-
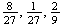 (b)
(b)
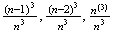 (c)
(c)
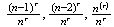
-
.018 (b) .020 (c) 18/78 = .231
-
.978
Chapter 3:
-
(a) 4/7
 (b) 5/42
(b) 5/42
 (c) 5/21;
(c) 5/21;
-
(a) (i)
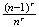 (ii)
(ii)
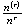
(b) All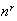 outcomes are equally likely. That is, all
outcomes are equally likely. That is, all
 floors are equally likely to be selected, and each passenger's selection is
unrelated to each other person's selection. Both assumptions are doubtful
since people may be travelling together (e.g. same family) and the floors may
not have equal traffic (e.g. more likely to use the stairs for going up 1
floor than for 10 floors);
floors are equally likely to be selected, and each passenger's selection is
unrelated to each other person's selection. Both assumptions are doubtful
since people may be travelling together (e.g. same family) and the floors may
not have equal traffic (e.g. more likely to use the stairs for going up 1
floor than for 10 floors);
-
(a) 5/18
 (b) 5/72;
(b) 5/72;
-
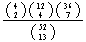
-
(a) 1/50,400
 (b) 7/45;
(b) 7/45;
-
(a) 1/6 (b) 0.12;
-
Values for
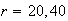 and 60 are .589, .109 and .006.
and 60 are .589, .109 and .006.
-
(a)
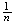 (b)
(b)
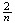
-
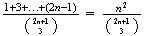
-
(a) (i) .0006 (ii) .0024 (b)
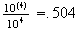
-
(a)
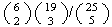 (b) 15
(b) 15
-
(a)
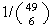 (b)
(b)
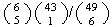 (c)
(c)
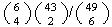 (d)
(d)
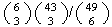
-
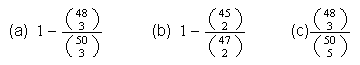
Chapter 4:
4.1 .75, .6, .65, 0, 1, .35, 14.2
 -
.01,
-
.01,
 - .72,
- .72,
 -
-
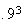 ,
,
 -
-
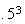 ,
,
 -
-
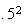
4.3
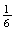
4.4 (a) 0.0576 (b) 0.4305 (c) 0.0168 (d) 0.5287
4.5 .44
4.6 0.7354
4.7 (a) .3087
 (b) .1852;
(b) .1852;

4.9 .342
4.10 (a) .1225, .175 (b) .395
4.11
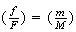
4.14 (a)
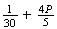 (b)
(b)
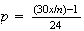 (c)
(c)
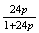
4.15 .9, .061, .078
4.16 (a) .024 (b) 8 on any one wheel and 1 on the others
4.17 (a) .995 and .005 (b) .001
4.18 (a) .99995 (b) .99889 (c\)
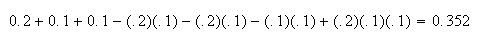
4.19 (a)
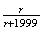 ;
;
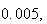
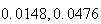 (b) 2.1%
(b) 2.1%
Chapter 5:
5.4 .545Chapter 6:
6.1 (a) .623, .251; for males, .408, .103 (b) .166
6.2 (a)
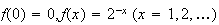 (b)
(b)
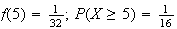
6.4
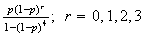
6.5 (a) .0800 (b) .171 (c) .00725
6.6 (a) .010 (b) .864
6.7 (a)
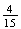 (b)
(b)
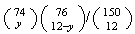 (c) .0176
(c) .0176
6.8 0.9989
6.9 (a) .0758 (b) .0488 (c)
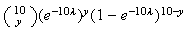 (d)
(d)
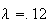
6.10 (a) .0769 (b) 0.2019; 0.4751
6.11 (a) 0.2753 (b) 0.1966 (c) 0.0215
6.12 (b) enables us to approximate hypergeometric distribution by binomial distribution when
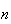 is large and
is large and
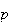 near 0.
near 0.
6.13 (a)
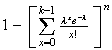 (b) (Could probably argue for other answers also). Budworms probably aren't
distributed at a uniform rate over the forest and may not occur singly
(b) (Could probably argue for other answers also). Budworms probably aren't
distributed at a uniform rate over the forest and may not occur singly
6.14 (a) .2048 (b) .0734 (c) .428 (d) .1404
6.15
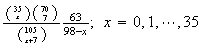
6.16 (a) .004264; .006669 (b) .0032 (c) (i)
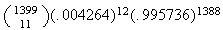
 (ii)
(ii)
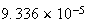
On the first 1399 attempts we essentially have a binomial distribution with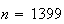 (large) and
(large) and
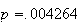 (near
(near
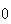 )
)
6.17 (a)
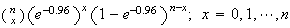 (b)
(b)
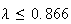 bubbles per
bubbles per
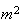
6.18
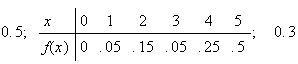
6.19 (a)
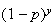 (b)
(b)
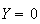 (c)
(c)
![$p/[1-(1-p)^{3}]$](graphics/noteschap10__636.png) (d)
(d)
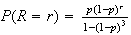 for
for
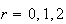
6.20 (a) .555 (b) .809; .965 (c) .789; .946 (d)
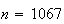
6.21 (a)
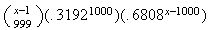 (b) .002, .051, .350, .797 (c)
(b) .002, .051, .350, .797 (c)
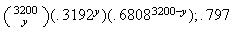
Chapter 7:
7.1 2.775; 2.574375
7.2 -$3
7.3 $16.90
7.4 (a) 3 cases (b) 32 cases
7.5 (a) - 10/37 dollars in both cases (b) .3442; 0.4865
7.6 $.94
7.7 (b)
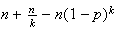 ,
which gives
,
which gives
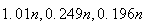 for
for
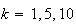
7.8 50
7.9 (a)
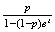 ;
(b)
;
(b)
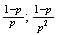
7.11 (a) Expand
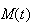 in a power series in powers of
in a power series in powers of
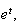 i.e.
i.e.
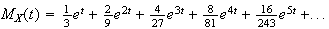 Then
Then
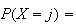 coefficient
of
coefficient
of
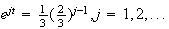 (b) Similarly
(b) Similarly
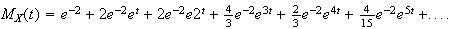 Then
Then
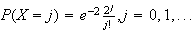
Chapter 8:
8.1 (a) no
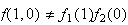 (b) 0.3 and 1/3
(b) 0.3 and 1/3
8.2 (a) mean = 0.15, variance = 0.15
8.3 (a) No (b) 0.978 (c) .05
8.4 (a)
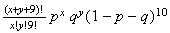 (b)
(b)
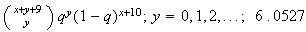
8.5 (b) - .10 dollars (c)
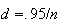
8.7
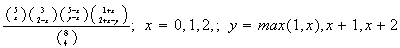 ;
(b) note e.g. that
;
(b) note e.g. that
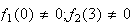 ,
but
,
but
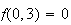
8.8 (a)
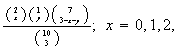 and
and
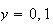 (b)
(b)
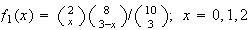 ;
;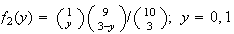 (c) 49/120 and 1/2
(c) 49/120 and 1/2
8.9 (a)
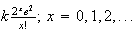 (b)
(b)
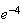 (c)
(c)
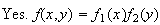
(d)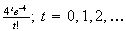
8.10 (b) .468
8.11 (a)
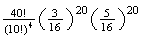 (b)
(b)
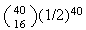 (c)
(c)
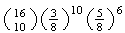
8.12 (a) 1.76 (b)
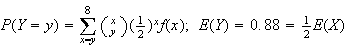
8.13 (a) Multinomial (b) .4602 (c) $5700
8.15 207.867
8.16 (a)
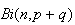 (b)
(b)
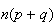 and
and
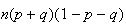 (c)
(c)
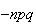
8.17 (a)
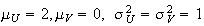 (b)
0
(b)
0
(c) no. e.g.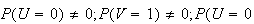 and
and
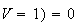
8.19 -1
8.20 (a) 1.22 (b) 17.67%
8.21
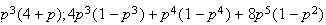
-
-
The transition matrix is
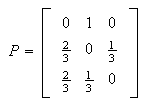 from which, solving
from which, solving
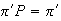 and rescaling so that the sum of the probabilities is one, we obtain
and rescaling so that the sum of the probabilities is one, we obtain
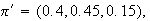 the long run fraction of time spent in cities A,B,C respectively.
the long run fraction of time spent in cities A,B,C respectively.
-
By arguments similar to those in section 8.3, the limiting matrix has rows all identically
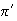 where the vector
where the vector
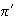 are the stationary probabilities satisfying
are the stationary probabilities satisfying
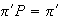 and
and
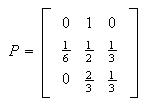 The solution is
The solution is
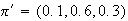 and the limit is
and the limit is

-
With
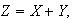
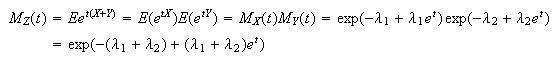 and since this is the MGF of a
Poisson(
and since this is the MGF of a
Poisson( distribution, this must be the distribution of
distribution, this must be the distribution of
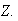
-
If today is raining, the probability of Rain, Nice, Snow three days from now is obtainable from the first row of the matrix
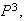 i.e.
i.e.
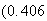
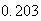
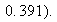 The
probabilities of the three states in five days, given (1) today is raining
(ii) today is nice (iii) today is snowing are the three rows of the matrix
The
probabilities of the three states in five days, given (1) today is raining
(ii) today is nice (iii) today is snowing are the three rows of the matrix
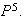 In this case call rows are identical to three decimals; they are all equal the
equilibrium distribution
In this case call rows are identical to three decimals; they are all equal the
equilibrium distribution
-
If a>b, and both parties raise then the probability B wins is
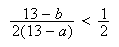 and the probability A wins is 1 minus this or
and the probability A wins is 1 minus this or
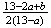 .
If
.
If
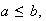 then the probability A wins is
then the probability A wins is
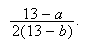
-
-
-
(a)
-
In the special case b=1, the expected winnings of A are
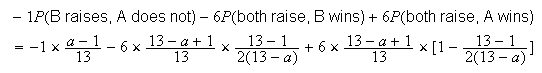 For a=1,2,...,13 this gives expected winnings of
0, 0.38462, 0.69231, 0.92308, 1.0769, 1.1538, 1.1538, 1.0769,
0.92308, 0.69231, 0.38462, 0, -0.46154 respectively, maximum for
a=6 or 7.
For a=1,2,...,13 this gives expected winnings of
0, 0.38462, 0.69231, 0.92308, 1.0769, 1.1538, 1.1538, 1.0769,
0.92308, 0.69231, 0.38462, 0, -0.46154 respectively, maximum for
a=6 or 7.
-
By a similar calculation as in part (b), A's possible winnings per game for a=1,2,...,13 are, respectively, -0.38462, -0.34615, -0.30769, -0.26923, -0.23077, -0.19231, -0.15385, -0.11538, -0.076923, -0.038462, 0, 0, -0.076923. There is no strategy that provides a positive expected return. The optimal is the break-even strategy a=11 or 12. (Note: in this two-person zero-sum game, a= 11 or 12 and b=11 or 12 is a minimax solution)
-
-
-
Show that you can determine the probability of the various values of
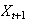 knowing only the state
knowing only the state
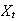 (and without knowing the previous states).
(and without knowing the previous states).
-
For example the long-run probability of the state
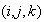 is, with
is, with
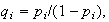
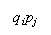
-
The probability that record
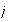 is in position
is in position
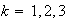 is, with
is, with
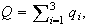
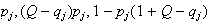 respectively. The expected cost of accessing a record in the long run is
respectively. The expected cost of accessing a record in the long run is
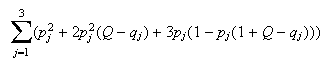 Substitute
Substitute
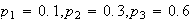 so
so
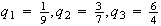 and
and
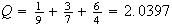 and (q8.28) is 1.7214.
and (q8.28) is 1.7214.
-
If they are in random order, the expected cost
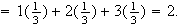 If they are ordered in terms of decreasing
If they are ordered in terms of decreasing
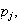 expected cost is
expected cost is
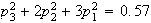
-
Chapter 9:
9.1
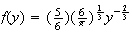 for
for
9.2 (a)
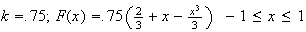
(b) Find such that
such that
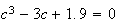 .
This gives
.
This gives
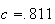
9.3 (a) 1/2, 1/24 (b) 0.2828 (c) 0.2043
9.4
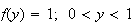
9.5 (a)
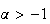 (b)
0.5
(b)
0.5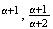 (c)
(c)
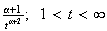
9.6 (a)
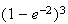 (b)
(b)
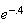
9.7
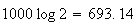
9.8 (a) .0668, .2417, .3829, .2417, .0668 (b) .0062 (c) .0771
9.9 (a) .5 (b)
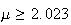
9.10 .4134
9.11 (a) .3868 (b) .6083 (c) 6.94
9.12 (a) .0062 (b) .9927
9.13 (a) .2327, .1841 (b) .8212, .8665; Guess if
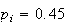 ,
don't guess if
,
don't guess if
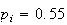
9.14 6.092 cents
9.15 574
9.16 (a) 7.6478, 88.7630 (b) 764.78, 8876.30, people within pooled samples are independent and each pooled sample is independent of each other pooled sample. (c) 0.3520
9.17 .5969
9.18 (a) .6728 (b) 250,088
9.19 (a)
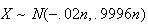 (b)
(b)
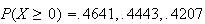 (using table) for
(using table) for
 The more you play, the smaller your chance of winning. (c)
1264.51
The more you play, the smaller your chance of winning. (c)
1264.51
With probability .99 the casino's profit is at least $1264.51.9.20 (a)
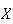 is approximately
is approximately
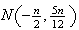 (b)
(i)
(b)
(i)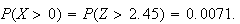 (ii)
(ii)
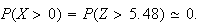
9.21 (a) (i) .202 (ii) .106 (b) .045, .048
9.22 (a) False positive probabilities are .048, .091, .023 for (i), (ii), (iii). False negative probabilities are .023, .091, .048.
-
-
Let
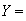 total
change over day. Given
total
change over day. Given
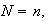
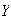 has a
Normal
has a
Normal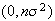 distribution and therefore
distribution and therefore
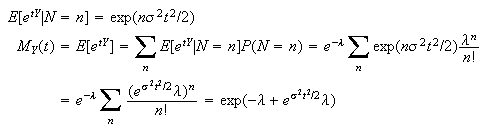 Not a MGF in this course at least. The mean is
Not a MGF in this course at least. The mean is
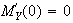 and the variance is
and the variance is
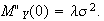
-
Summary of Distributions
Probabilities For the Standard Normal DistributionDiscrete Notation and Parameters Probability function 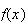
Mean Variance Moment generating function 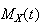
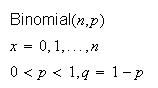
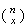
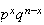
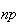
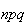
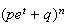
Bernoulli 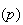
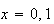
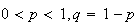
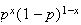
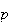
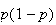
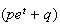
Negative Binomial 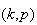
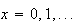
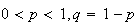
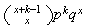
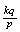
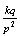
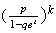
Geometric 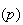
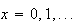
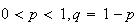
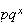
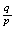
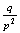
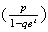
Hypergeometric 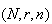
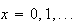 min(
min(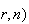
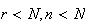
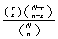
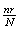
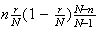
intractible Poisson 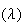
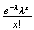
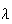
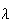
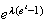
Continuous p.d.f. 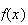
Mean Variance Moment generating function 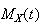
Uniform 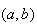
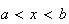
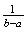
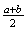
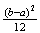
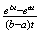
Exponential 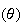
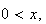
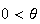
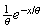
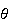
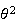
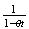
Normal 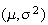
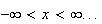
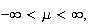
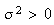
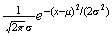
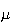
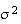
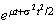
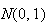
-
-
-