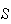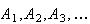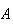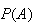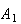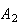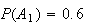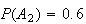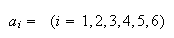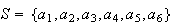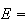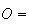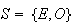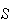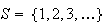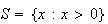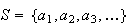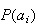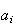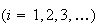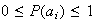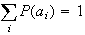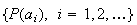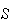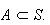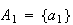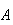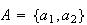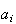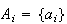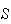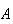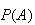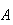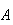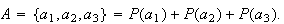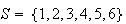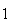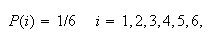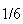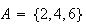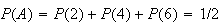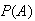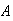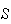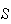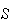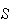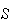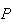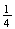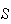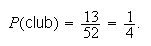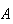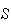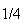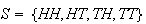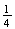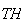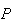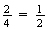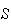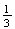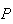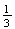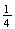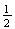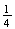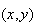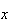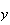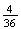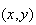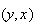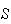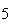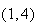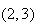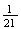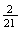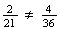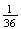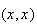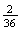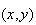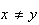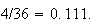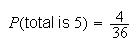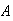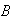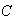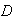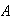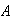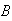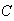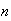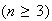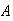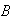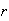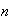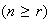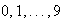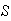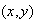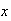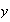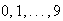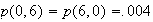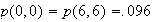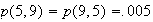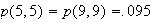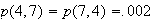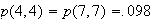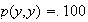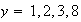1. Introduction to Probability
In some areas, such as mathematics or logic, results of some process can be
known with certainty (e.g., 2+3=5). Most real life situations, however,
involve variability and uncertainty. For example, it is uncertain whether it
will rain tomorrow; the price of a given stock a week from today is
uncertain Note_1 ; the number of
claims that a car insurance policy holder will make over a one-year period is
uncertain. Uncertainty or "randomness" (meaning variability of results) is
usually due to some mixture of two factors: (1) variability in populations
consisting of animate or inanimate objects (e.g., people vary in size, weight,
blood type etc.), and (2) variability in processes or phenomena (e.g., the
random selection of 6 numbers from 49 in a lottery draw can lead to a very
large number of different outcomes; stock or currency prices fluctuate
substantially over time).
Variability and uncertainty make it more difficult to plan or to make
decisions. Although they cannot usually be eliminated, it is however possible
to describe and to deal with variability and uncertainty, by using the theory
of probability. This course develops both the theory and applications of
probability.
It seems logical to begin by defining probability. People have attempted to do
this by giving definitions that reflect the uncertainty whether some specified
outcome or ``event" will occur in a given setting. The setting is often termed
an ``experiment" or ``process" for the sake of discussion. To take a simple
``toy" example: it is uncertain whether the number 2 will turn up when a
6-sided die is rolled. It is similarly uncertain whether the Canadian dollar
will be higher tomorrow, relative to the U.S. dollar, than it is today. Three
approaches to defining probability are:
-
The classical definition: Let the sample
space (denoted by
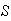 )
be the set of all possible distinct outcomes to an experiment. The probability
of some event is
)
be the set of all possible distinct outcomes to an experiment. The probability
of some event is
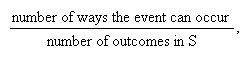 provided all points in
provided all points in
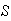 are equally likely. For example, when a die is rolled the probability of
getting a 2 is
are equally likely. For example, when a die is rolled the probability of
getting a 2 is
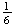 because one of the six faces is a 2.
because one of the six faces is a 2.
-
The relative frequency definition: The probability of an
event is the proportion (or fraction) of times the event occurs in a very long
(theoretically infinite) series of repetitions of an experiment or process.
For example, this definition could be used to argue that the probability of
getting a 2 from a rolled die is
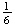 .
.
-
The subjective probability definition: The probability of an
event is a measure of how sure the person making the statement is that the
event will happen. For example, after considering all available data, a
weather forecaster might say that the probability of rain today is 30% or
0.3.
Unfortunately, all three of these definitions have serious
limitations.
Classical Definition:
What does "equally likely" mean? This appears to use the concept of
probability while trying to define it! We could remove the phrase "provided
all outcomes are equally likely", but then the definition would clearly be
unusable in many settings where the outcomes in
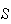 did not tend to occur equally often.
did not tend to occur equally often.
Relative Frequency Definition:
Since we can never repeat an experiment or process indefinitely, we can never
know the probability of any event from the relative frequency definition. In
many cases we can't even obtain a long series of repetitions due to time,
cost, or other limitations. For example, the probability of rain today can't
really be obtained by the relative frequency definition since today can't be
repeated again.
Subjective Probability:
This definition gives no rational basis for people to agree on a right answer.
There is some controversy about when, if ever, to use subjective probability
except for personal decision-making. It will not be used in Stat
230.
These difficulties can be overcome by treating probability as a mathematical
system defined by a set of axioms. In this case we do not worry about the
numerical values of probabilities until we consider a specific application.
This is consistent with the way that other branches of mathematics are defined
and then used in specific applications (e.g., the way calculus and real-valued
functions are used to model and describe the physics of gravity and motion).
The mathematical approach that we will develop and use in the remaining
chapters assumes the following:
-
probabilities are numbers between 0 and 1 that apply to outcomes, termed
``events'',
-
each event may or may not occur in a given setting.
Chapter 2 begins by specifying the mathematical framework for probability in
more detail.
Exercises
-
Try to think of examples of probabilities you have encountered which might
have been obtained by each of the three ``definitions".
-
Which definitions do you think could be used for obtaining the following
probabilities?
-
You have a claim on your car insurance in the next year.
-
There is a meltdown at a nuclear power plant during the next 5 years.
-
A person's birthday is in April.
-
Give examples of how probability applies to each of the following areas.
-
Lottery draws
-
Auditing of expense items in a financial statement
-
Disease transmission (e.g. measles, tuberculosis, STD's)
-
Public opinion polls
2. Mathematical Probability Models
Sample Spaces and Probability
Consider some phenomenon or process which is repeatable, at least in theory,
and suppose that certain events (outcomes)
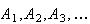 are defined. We will often term the phenomenon or process an
``experiment" and refer to a single repetition of the
experiment as a ``trial". Then the probability of an event
are defined. We will often term the phenomenon or process an
``experiment" and refer to a single repetition of the
experiment as a ``trial". Then the probability of an event
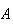 ,
denoted
,
denoted
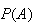 ,
is a number between 0 and 1.
,
is a number between 0 and 1.
If probability is to be a useful mathematical concept, it should possess some
other properties. For example, if our ``experiment'' consists of tossing a
coin with two sides, Head and Tail, then we might wish to consider the events
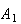 = ``Head turns up'' and
= ``Head turns up'' and
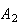 = ``Tail turns up''. It would clearly not be desirable to allow, say,
= ``Tail turns up''. It would clearly not be desirable to allow, say,
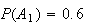 and
and
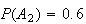 ,
so that
,
so that
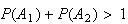 .
(Think about why this is so.) To avoid this sort of thing we begin with the
following definition.
.
(Think about why this is so.) To avoid this sort of thing we begin with the
following definition.
Definition
A sample space
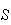 is a set of distinct outcomes for an experiment or process, with the property
that in a single trial, one and only one of these outcomes occurs. The
outcomes that make up the sample space are called sample
points.
is a set of distinct outcomes for an experiment or process, with the property
that in a single trial, one and only one of these outcomes occurs. The
outcomes that make up the sample space are called sample
points.
A sample space is part of the probability model in a given setting. It is not
necessarily unique, as the following example shows.
Example: Roll a 6-sided die, and define the events
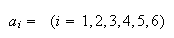 Then we could take the sample space as
Then we could take the sample space as
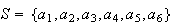 .
However, we could also define events
.
However, we could also define events
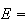 |
even number turns up |
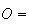 |
odd number turns up |
and take
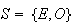 .
Both sample spaces satisfy the definition, and which one we use would depend
on what we wanted to use the probability model for. In most cases we would use
the first sample space.
.
Both sample spaces satisfy the definition, and which one we use would depend
on what we wanted to use the probability model for. In most cases we would use
the first sample space.
Sample spaces may be either discrete or
non-discrete;
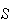 is discrete if it consists of a finite or countably infinite set of simple
events. The two sample spaces in the preceding example are discrete. A sample
space
is discrete if it consists of a finite or countably infinite set of simple
events. The two sample spaces in the preceding example are discrete. A sample
space
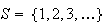 consisting of all the positive integers is also, for example, discrete, but a
sample space
consisting of all the positive integers is also, for example, discrete, but a
sample space
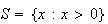 consisting of all positive real numbers is not. For the next few chapters we
consider only discrete sample spaces. This makes it easier to define
mathematical probability, as follows.
consisting of all positive real numbers is not. For the next few chapters we
consider only discrete sample spaces. This makes it easier to define
mathematical probability, as follows.
-
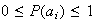
-
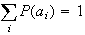
The set of values
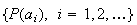 is called a probability distribution on
is called a probability distribution on
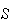 .
.
Our notation will often not distinguish between the point
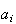 and the simple event
and the simple event
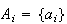 which has this point as its only element, although they differ as mathematical
objects. The condition (2) in the definition above reflects the idea that when
the process or experiment happens, some event in
which has this point as its only element, although they differ as mathematical
objects. The condition (2) in the definition above reflects the idea that when
the process or experiment happens, some event in
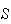 must occur (see the definition of sample space). The probability of a more
general event
must occur (see the definition of sample space). The probability of a more
general event
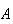 (not necessarily a simple event) is then defined as follows:
(not necessarily a simple event) is then defined as follows:
For example, the probability of the compound event
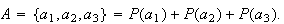 The definition of probability does not say what numbers to assign to the
simple events for a given setting, only what properties the numbers must
possess. In an actual situation, we try to specify numerical values that make
the model useful; this usually means that we try to specify numbers that are
consistent with one or more of the empirical ``definitions'' of Chapter
1.
The definition of probability does not say what numbers to assign to the
simple events for a given setting, only what properties the numbers must
possess. In an actual situation, we try to specify numerical values that make
the model useful; this usually means that we try to specify numbers that are
consistent with one or more of the empirical ``definitions'' of Chapter
1.
Example: Suppose a 6-sided die is rolled, and let the sample
space be
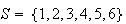 ,
where
,
where
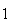 means the number 1 occurs, and so on. If the die is an ordinary one, we would
find it useful to define probabilities as
means the number 1 occurs, and so on. If the die is an ordinary one, we would
find it useful to define probabilities as
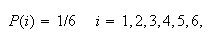 because if the die were tossed repeatedly (as in some games or gambling
situations) then each number would occur close to
because if the die were tossed repeatedly (as in some games or gambling
situations) then each number would occur close to
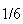 of the time. However, if the die were weighted in some way, these numerical
values would not be so useful.
of the time. However, if the die were weighted in some way, these numerical
values would not be so useful.
Note that if we wish to consider some compound event, the probability is
easily obtained. For example, if
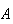 = ``even number" then because
= ``even number" then because
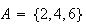 we get
we get
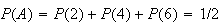 .
.
We now consider some additional examples, starting with some simple ``toy"
problems involving cards, coins and dice and then considering a more
scientific example.
Remember that in using probability we are actually constructing mathematical
models. We can approach a given problem by a series of three steps:
-
Specify a sample space
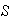 .
.
-
Assign numerical probabilities to the simple events in
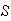 .
.
-
For any compound event
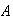 ,
find
,
find
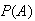 by adding the probabilities of all the simple events that make up
by adding the probabilities of all the simple events that make up
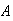 .
.
Many probability problems are stated as ``Find the probability that ...''. To
solve the problem you should then carry out step (2) above by assigning
probabilities that reflect long run relative frequencies of occurrence of the
simple events in repeated trials, if possible.
Some Examples
When
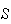 has few points, one of the easiest methods for finding the probability of an
event is to list all outcomes. In many problems a sample space
has few points, one of the easiest methods for finding the probability of an
event is to list all outcomes. In many problems a sample space
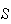 with equally probable simple events can be used, and the first few examples
are of this type.
with equally probable simple events can be used, and the first few examples
are of this type.
Example: Draw 1 card from a standard well-shuffled deck
(13 cards of each of 4 suits - spades, hearts, diamonds, clubs). Find the
probability the card is a club.
Solution 1: Let
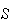 = { spade, heart, diamond, club}. (The points of
= { spade, heart, diamond, club}. (The points of
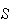 are generally listed between brackets {}.) Then
are generally listed between brackets {}.) Then
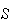 has 4 points, with 1 of them being "club", so
has 4 points, with 1 of them being "club", so
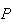 (club)
=
(club)
=
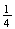 .
.
Solution 2: Let
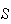 = {each of the 52 cards}. Then 13 of the 52 cards are clubs, so
= {each of the 52 cards}. Then 13 of the 52 cards are clubs, so
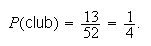
Note 1: A sample space is not necessarily unique, as
mentioned earlier. The two solutions illustrate this. Note that in the first
solution the event
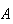 = "the card is a club" is a simple event, but in the second it is a compound
event.
= "the card is a club" is a simple event, but in the second it is a compound
event.
Note 2: In solving the problem we have assumed that each
simple event in
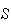 is equally probable. For example in Solution 1 each simple event has
probability
is equally probable. For example in Solution 1 each simple event has
probability
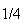 .
This seems to be the only sensible choice of numerical value in this setting.
(Why?)
.
This seems to be the only sensible choice of numerical value in this setting.
(Why?)
Note 3: The term "odds" is sometimes used. The odds of an
event is the probability it occurs divided by the probability it does not
occur. In this card example the odds in favour of clubs are 1:3; we could also
say the odds against clubs are 3:1.
Example: Toss a coin twice. Find the probability of getting
1 head. (In this course, 1 head is taken to mean exactly 1
head. If we meant at least 1 head we would say
so.)
Solution 1: Let
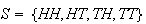 and assume the simple events each have probability
and assume the simple events each have probability
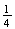 .
(If your notation is not obvious, please explain it. For example,
.
(If your notation is not obvious, please explain it. For example,
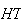 means head on the
means head on the
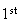 toss and tails on the
toss and tails on the
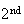 .)
Since 1 head occurs for simple events
.)
Since 1 head occurs for simple events
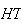 and
and
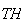 ,
we get
,
we get
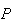 (1 head) =
(1 head) =
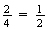 .
.
Solution 2: Let
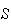 = { 0 heads, 1 head, 2 heads } and assume the simple events each have
probability
= { 0 heads, 1 head, 2 heads } and assume the simple events each have
probability
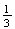 .
Then
.
Then
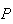 (1
head) =
(1
head) =
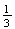 .
.

|
9 tosses of two coins
each
|
Which solution is right? Both are mathematically "correct". However, we want a
solution that is useful in terms of the probabilities of events reflecting
their relative frequency of occurrence in repeated trials. In that sense, the
points in solution 2 are not equally likely. The outcome 1 head occurs more
often than either 0 or 2 heads in actual repeated trials. You can experiment
to verify this (for example of the nine replications of the experiment in
Figure coins, 2 heads occurred 2 of the nine times,
1 head occurred 6 of the 9 times. For more certainty you should replicate this
experiment many times. You can do this without benefit of coin at
http://shazam.econ.ubc.ca/flip/index.html). So we say solution 2 is incorrect
for ordinary physical coins though a better term might be "incorrect model".
If we were determined to use the sample space in solution 2, we could do it by
assigning appropriate probabilities to each point. From solution 1, we can see
that 0 heads would have a probability of
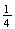 ,
1 head
,
1 head
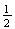 ,
and 2 heads
,
and 2 heads
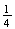 .
However, there seems to be little point using a sample space whose points are
not equally probable when one with equally probable points is readily
available.
.
However, there seems to be little point using a sample space whose points are
not equally probable when one with equally probable points is readily
available.
Example: Roll a red die and a green die. Find the
probability the total is 5.
Solution: Let
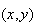 represent getting
represent getting
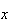 on the red die and
on the red die and
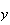 on the green die.
on the green die.
Then, with these as simple events, the sample space is
 The sample points giving a total of 5 are (1,4) (2,3) (3,2), and (4,1).
The sample points giving a total of 5 are (1,4) (2,3) (3,2), and (4,1).
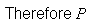 (total is 5) =
(total is 5) =
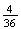
Example: Suppose the 2 dice were now identical red dice.
Find the probability the total is 5.
Solution 1: Since we can no longer distinguish between
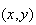 and
and
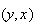 ,
the only distinguishable points in
,
the only distinguishable points in
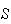 are :
are :

Using this sample space, we get a total of
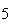 from points
from points
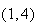 and
and
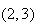 only. If we assign equal probability
only. If we assign equal probability
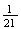 to each point (simple event) then we get
to each point (simple event) then we get
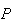 (total
is 5) =
(total
is 5) =
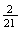 .
.
At this point you should be suspicious since
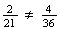 .
The colour of the dice shouldn't have any effect on what total we get, so this
answer must be wrong. The problem is that the 21 points in
.
The colour of the dice shouldn't have any effect on what total we get, so this
answer must be wrong. The problem is that the 21 points in
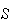 here are not equally likely. If this experiment is repeated, the point (1, 2)
occurs twice as often in the long run as the point (1,1). The only sensible
way to use this sample space would be to assign probability weights
here are not equally likely. If this experiment is repeated, the point (1, 2)
occurs twice as often in the long run as the point (1,1). The only sensible
way to use this sample space would be to assign probability weights
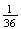 to the points
to the points
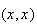 and
and
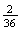 to the points
to the points
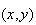 for
for
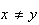 .
Of course we can compare these probabilities with experimental evidence. On
the website
http://www.math.duke.edu/education/postcalc/probability/dice/index.html you
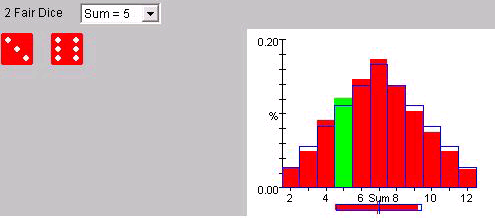
may throw dice up to 10,000 times and record the results. For example on 1000
throws of two dice (see Figure 2dice), there were 121
occasions when the sum of the values on the dice was 5, indicating the
probability is around 121/1000 or 0.121 This compares with the true
probability
.
Of course we can compare these probabilities with experimental evidence. On
the website
http://www.math.duke.edu/education/postcalc/probability/dice/index.html you
may throw dice up to 10,000 times and record the results. For example on 1000
throws of two dice (see Figure 2dice), there were 121
occasions when the sum of the values on the dice was 5, indicating the
probability is around 121/1000 or 0.121 This compares with the true
probability
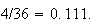
|
Results of 1000 throws of 2
dice
|
A more straightforward
solution
follows.
Solution 2: Pretend the dice can be distinguished even
though they can't. (Imagine, for example, that we put a white dot on one die,
or label one of them 1 and the other as 2.) We then get the same 36 sample
points as in the example with the red die and the green die.
Hence
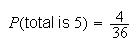 But, you argue, the dice were identical, and you cannot distinguish them! The
laws determining the probabilities associated with these two dice do not, of
course, know whether your eyesight is so keen that you can or cannot
distinguish the dice. These probabilities must be the same in either case. In
many cases, when objects are indistinguishable and we are interested in
calculating a probability, the calculation is made easier by pretending the
objects can be distinguished.
But, you argue, the dice were identical, and you cannot distinguish them! The
laws determining the probabilities associated with these two dice do not, of
course, know whether your eyesight is so keen that you can or cannot
distinguish the dice. These probabilities must be the same in either case. In
many cases, when objects are indistinguishable and we are interested in
calculating a probability, the calculation is made easier by pretending the
objects can be distinguished.
This illustrates a common
pitfall in using probability. When treating objects in an experiment as
distinguishable leads to a different answer from treating them as identical,
the points in the sample space for identical objects are usually not ``equally
likely" in terms of their long run relative frequencies. It is generally safer
to pretend objects can be distinguished even when they can't be, in order to
get equally likely sample points.
While the method of finding probability by listing all the points in
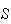 can be useful, it isn't practical when there are a lot of points to write out
(e.g., if 3 dice were tossed there would be 216 points in
can be useful, it isn't practical when there are a lot of points to write out
(e.g., if 3 dice were tossed there would be 216 points in
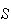 ).
We need to have more efficient ways of figuring out the number of outcomes in
).
We need to have more efficient ways of figuring out the number of outcomes in
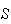 or in a compound event without having to list them all. Chapter 3 considers
ways to do this, and then Chapter 4 develops other ways to manipulate and
calculate probabilities.
or in a compound event without having to list them all. Chapter 3 considers
ways to do this, and then Chapter 4 develops other ways to manipulate and
calculate probabilities.
To conclude this chapter, we remark that in some settings we rely on previous
repetitions of an experiment, or on scientific data, to assign numerical
probabilities to events. Problems 2.6 and 2.7 below illustrate this. Although
we often use "toy" problems involving things such as coins, dice and simple
games for examples, probability is used to deal with a huge variety of
practical problems. Problems 2.6 and 2.7, and many others to be discussed
later, are of this type.
Problems on Chapter 2
-
Students in a particular program have the same 4 math profs. Two students in
the program each independently ask one of their math profs for a letter of
reference. Assume each is equally likely to ask any of the math profs.
-
List a sample space for this ``experiment''.
-
Use this sample space to find the probability both students ask the same prof.
-
-
List a sample space for tossing a fair coin 3 times.
-
What is the probability of 2 consecutive tails (but not 3)?
-
You wish to choose 2 different numbers from 1, 2, 3, 4, 5. List all possible
pairs you could obtain and find the probability the numbers chosen differ by 1
(i.e. are consecutive).
-
Four letters addressed to individuals
 ,
,
 ,
,
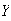 and
and
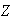 are randomly placed in four addressed envelopes, one letter in each envelope.
are randomly placed in four addressed envelopes, one letter in each envelope.
-
List a 24-point sample space for this experiment.
-
List the sample points belonging to each of the following events:
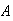 :
``
:
``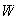 's
letter goes into the correct envelope'';
's
letter goes into the correct envelope'';
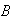 :
``no letters go into the correct envelopes'';
:
``no letters go into the correct envelopes'';
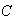 :
``exactly two letters go into the correct envelopes'';
:
``exactly two letters go into the correct envelopes'';
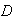 :
``exactly three letters go into the correct envelopes''.
:
``exactly three letters go into the correct envelopes''.
-
Assuming that the 24 sample points are equally probable, find the
probabilities of the four events in (b).
-
-
Three balls are placed at random in three boxes, with no restriction on the
number of balls per box; list the 27 possible outcomes of this experiment.
Assuming that the outcomes are all equally probable, find the probability of
each of the following events:
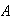 :
``the first box is empty'';
:
``the first box is empty'';
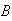 :
``the first two boxes are empty'';
:
``the first two boxes are empty'';
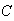 :
``no box contains more than one ball''.
:
``no box contains more than one ball''.
-
Find the probabilities of events
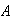 ,
,
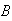 and
and
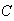 when three balls are placed at random in
when three balls are placed at random in
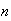 boxes
boxes
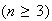 .
.
-
Find the probabilities of events
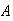 ,
,
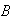 and
and
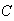 when
when
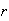 balls are placed in
balls are placed in
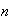 boxes
boxes
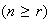 .
.
-
Diagnostic Tests. Suppose that in a large population some
persons have a specific disease at a given point in time. A person can be
tested for the disease, but inexpensive tests are often imperfect, and may
give either a ``false positive'' result (the person does not have the disease
but the test says they do) or a ``false negative'' result (the person has the
disease but the test says they do not).
In a random sample of 1000
people, individuals with the disease were identified according to a completely
accurate but expensive test, and also according to a less accurate but
inexpensive test. The results for the less accurate test were that
-
920 persons without the disease tested negative
-
60 persons without the disease tested positive
-
18 persons with the disease tested positive
-
2 persons with the disease tested negative.
(a)-
Estimate the fraction of the population that has the disease and tests
positive using the inexpensive test.
-
Estimate the fraction of the population that has the disease.
-
Suppose that someone randomly selected from the population tests positive
using the inexpensive test. Estimate the probability that they actually have
the disease.
-
Machine Recognition of Handwritten Digits. Suppose that you
have an optical scanner and associated software for determining which of the
digits
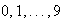 an individual has written in a square box. The system may of course be wrong
sometimes, depending on the legibility of the handwritten number.
an individual has written in a square box. The system may of course be wrong
sometimes, depending on the legibility of the handwritten number.
-
Describe a sample space
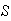 that includes points
that includes points
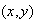 ,
where
,
where
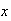 stands for the number actually written, and
stands for the number actually written, and
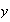 stands for the number that the machine identifies.
stands for the number that the machine identifies.
-
Suppose that the machine is asked to identify very large numbers of digits, of
which
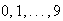 occur equally often, and suppose that the following probabilities apply to the
points in your sample space:
occur equally often, and suppose that the following probabilities apply to the
points in your sample space:
Give a table with probabilities for each point
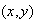 in
in
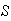 .
What fraction of numbers is correctly identified?
.
What fraction of numbers is correctly identified?
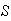 )
be the set of all possible distinct outcomes to an experiment. The probability
of some event is
)
be the set of all possible distinct outcomes to an experiment. The probability
of some event is
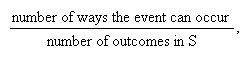 provided all points in
provided all points in
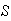 are equally likely. For example, when a die is rolled the probability of
getting a 2 is
are equally likely. For example, when a die is rolled the probability of
getting a 2 is
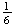 because one of the six faces is a 2.
because one of the six faces is a 2.
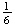 .
.