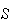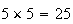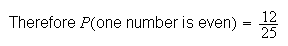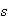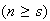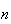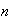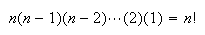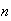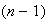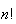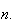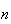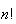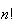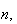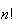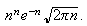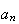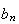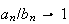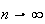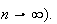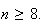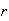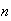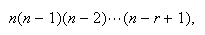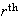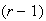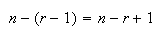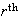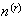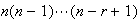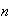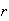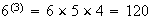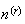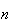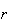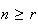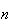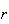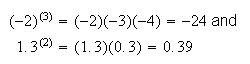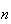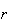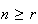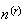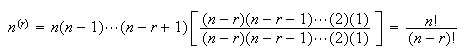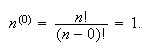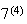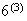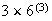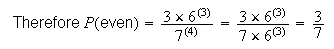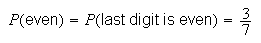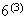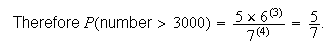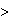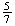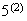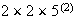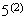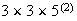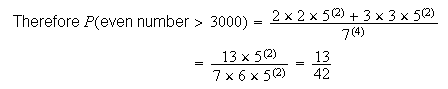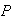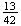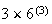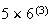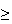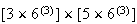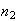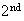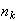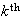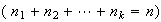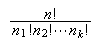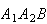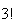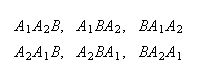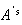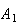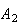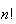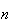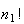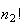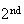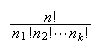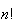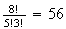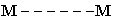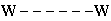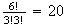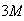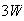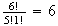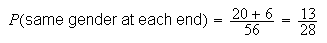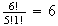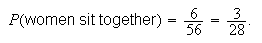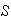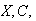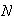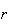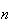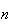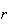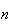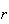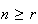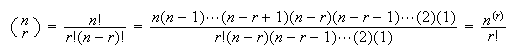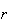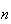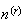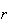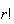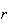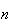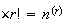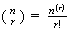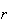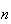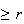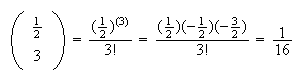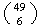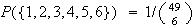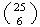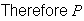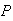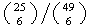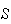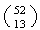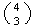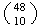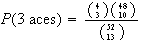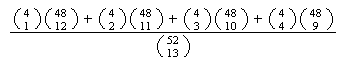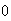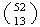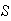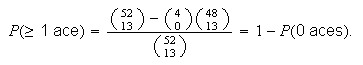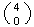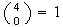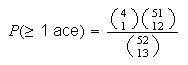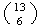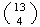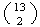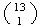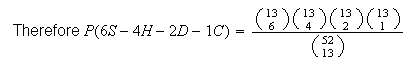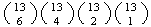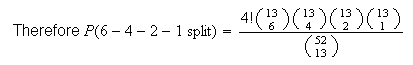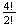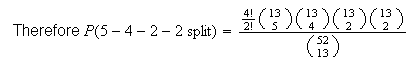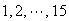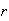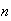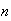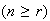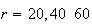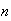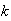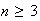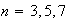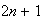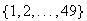-
-
A course has 4 sections with no limit on how many can enrol in each section. 3
students each randomly pick a section. Find the probability:
-
they all end up in the same section
-
they all end up in different sections
-
nobody picks section 1.
-
Repeat (a) in the case when there are
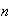 sections and
sections and
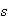 students
students
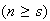 .
.
-
Canadian postal codes consist of 3 letters alternated with 3 digits, starting
with a letter (e.g. N2L 3G1). For a randomly constructed postal code, what is
the probability:
-
all 3 letters are the same?
-
the digits are all even or all odd? Treat 0 as being neither even nor odd.
-
Suppose a password has to contain between six and eight digits, with each
digit either a letter or a number from 1 to 9. There must be at least one
number present.
-
What is the total number of possible passwords?
-
If you started to try passwords in random order, what is the probability you
would find the correct password for a given situation within the first 1,000
passwords you tried?
Permutation Rules
Suppose that
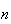 distinct objects are to be ``drawn" sequentially, or ordered from left to
right in a row.
distinct objects are to be ``drawn" sequentially, or ordered from left to
right in a row.
(Order matters; objects are drawn without replacement)
-
The number of ways to arrange
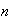 distinct
objects in a row
is
distinct
objects in a row
is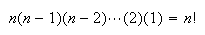
Explanation: We can fill the first position in
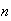 ways. Since this object can't be used again, there are only
ways. Since this object can't be used again, there are only
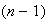 ways to fill the second position. So we keep having 1 fewer object available
after each position is filled.
ways to fill the second position. So we keep having 1 fewer object available
after each position is filled.
Statistics is important, and many games are interesting largely because of the
extraordinary rate of growth of the function
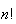 in
in
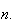 For
example
For
example
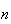 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
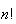 |
1 |
1 |
2 |
6 |
24 |
120 |
720 |
5040 |
40320 |
362880 |
3628800 |
which means that for many problems involving sampling from a deck of cards or
a reasonably large population, counting the number of cases is virtually
impossible. There is an approximation to
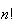 which is often used for large
which is often used for large
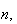 called Stirling's formula which says that
called Stirling's formula which says that
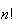 is asymptotic to
is asymptotic to
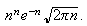 Here, two sequences
Here, two sequences
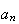 and
and
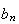 are called asymptotically equal if
are called asymptotically equal if
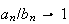 as
as
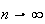 (intuitively, the percentage error in using Stirling's approximation goes to
zero as
(intuitively, the percentage error in using Stirling's approximation goes to
zero as
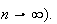 For
example the error in Stirling's approximation is less than 1% if
For
example the error in Stirling's approximation is less than 1% if
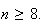
-
The number of ways to arrange
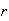 objects
selected from
objects
selected from
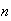 distinct
objects is
distinct
objects is
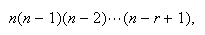 using the same reasoning as in #1, and noting that for the
using the same reasoning as in #1, and noting that for the
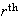 selection,
selection,
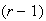 objects have already been used. Hence there
are
objects have already been used. Hence there
are
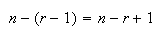 ways to make the
ways to make the
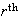 selection. We use the symbol
selection. We use the symbol
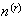 to represent
to represent
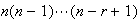 and describe this symbol as
"
and describe this symbol as
"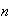 taken to
taken to
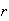 terms". E.g.
terms". E.g.
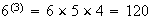 .
.
While
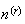 only has a physical interpretation when
only has a physical interpretation when
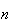 and
and
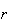 are positive integers with
are positive integers with
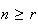 ,
it still has a mathematical meaning when
,
it still has a mathematical meaning when
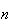 is not a positive integer, as long as
is not a positive integer, as long as
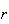 is a non-negative integer. For example
is a non-negative integer. For example
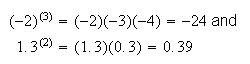
We will occasionally encounter such cases in this course but generally
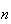 and
and
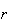 will be non-negative integers with
will be non-negative integers with
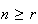 .
In this case, we can re-write
.
In this case, we can re-write
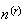 in terms of factorials.
in terms of factorials.
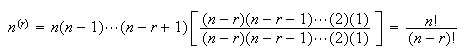 Note
that
Note
that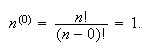
The idea in using counting methods is to break the experiment into pieces or
``jobs'' so that counting rules can be applied. There is usually more than one
way to do this.
Example: We form a 4 digit number by randomly selecting and
arranging 4 digits from 1, 2, 3,...7 without replacement. Find the probability
the number formed is (a) even (b) over 3000 (c) an even number over
3000.
Solution: Let
 be the set of all possible 4 digit numbers using digits 1, 2, ..., 7 without
repetitions.
be the set of all possible 4 digit numbers using digits 1, 2, ..., 7 without
repetitions.
Then
 has
has
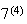 points. (We could calculate this but it will be easier to leave it in this
form for now and do some cancelling later.)
points. (We could calculate this but it will be easier to leave it in this
form for now and do some cancelling later.)
-
For a number to be even, the last digit must be even. We can fill this last
position with a 2, 4, or 6; i.e. in 3 ways. The first 3 positions can be
filled by choosing and arranging 3 of the 6 digits not used in the final
position. i.e. in
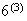 ways. Then there are
ways. Then there are
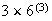 ways to fill the final position AND the first 3 positions to produce an even
number.
ways to fill the final position AND the first 3 positions to produce an even
number.
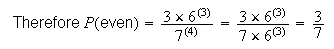
Another way to do this problem is to note that the four digit number is even
if and only if (iff) the last digit is even. The last digit is equally likely
to be any one of the numbers 1, ..., 7 so
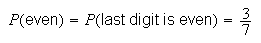
-
To get a number over 3000, we require the first digit to be 3, 4, 5, 6, or 7;
i.e. it can be chosen in 5 ways. The remaining 3 positions can be filled in
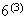 ways.
ways.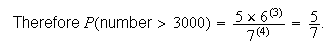
Another way to do this problem is to note that the four digit number is over
3000 iff the first digit is one of 3, 4, 5, 6 or 7. Since each of 1, ..., 7 is
equally likely to be the first digit, we get
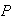 (number
(number
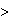 3000) =
3000) =
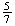 .
.
Note that in both (a) and (b) we dealt with positions which had restrictions
first, before considering positions with no restrictions. This is generally
the best approach to follow in applying counting techniques.
-
This part has restrictions on both the first and last positions. To illustrate
the complication this introduces, suppose we decide to fill positions in the
order 1 then 4 then the middle two. We can fill position 1 in 5 ways. How many
ways can we then fill position 4? The answer is either 2 or 3 ways, depending
on whether the first position was filled with an even or odd digit. Whenever
we encounter a situation such as this, we have to break the solution into
separate cases. One case is where the first digit is even. The positions can
be filled in 2 ways for the first (i.e. with a 4 or 6), 2 ways for the last,
and then
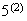 ways to arrange 2 of the remaining 5 digits in the middle positions. This
first case then occurs in
ways to arrange 2 of the remaining 5 digits in the middle positions. This
first case then occurs in
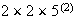 ways. The second case has an odd digit in position one. There are 3 ways to
fill position one (3, 5, or 7), 3 ways to fill position four (2, 4, or 6), and
ways. The second case has an odd digit in position one. There are 3 ways to
fill position one (3, 5, or 7), 3 ways to fill position four (2, 4, or 6), and
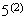 ways to fill the remaining positions. Case 2 then occurs in
ways to fill the remaining positions. Case 2 then occurs in
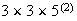 ways. We need case 1 OR case 2.
ways. We need case 1 OR case 2.
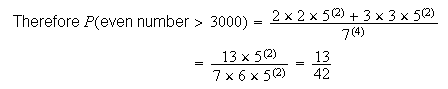
Another way to do this is to realize that we need only to consider the first
and last digit, and to find
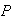 (first
digit is
(first
digit is
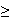 3 and last digit is even). There are
3 and last digit is even). There are
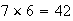 different choices for (first digit, last digit) and it is easy to see there
are 13 choices for which first digit
different choices for (first digit, last digit) and it is easy to see there
are 13 choices for which first digit
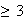 ,
last digit is even (
,
last digit is even (
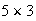 minus the impossible outcomes (4, 4) and (6, 6)). Thus the desired probability
is
minus the impossible outcomes (4, 4) and (6, 6)). Thus the desired probability
is
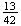 .
.
Exercise: Try to solve part (c) by filling positions in
the order 4, 1, middle. You should get the same answer.
Exercise: Can you spot the flaw in the following?
There are
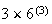 ways to get an even number (part (a))
ways to get an even number (part (a))
There are
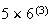 ways to get a number
ways to get a number
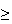 3000 (part (b))
3000 (part (b))
By the multiplication rule there are
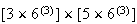 ways to get a number which is even and
ways to get a number which is even and
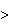 3000. (Read the conditions in the multiplication rule carefully, if you
believe this solution.)
3000. (Read the conditions in the multiplication rule carefully, if you
believe this solution.)
Here is another useful rule.
-
The number of distinct arrangements of
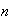 objects
when
objects
when
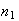 are
alike of one type,
are
alike of one type,
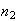 alike
of a
alike
of a
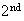 type,
...,
type,
...,
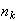 alike
of a
alike
of a
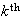 type
type
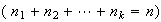 is
is
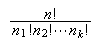
For example: We can arrange
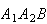 in
in
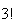 ways. These are
ways. These are
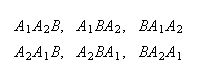
However, as soon as we remove the subscripts on the
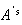 ,
the second row is the same as the first row. I.e., we have only 3 distinct
arrangements since each arrangement appears twice as the
,
the second row is the same as the first row. I.e., we have only 3 distinct
arrangements since each arrangement appears twice as the
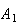 and
and
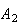 are interchanged. In general, there would be
are interchanged. In general, there would be
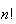 arrangements if all
arrangements if all
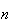 objects were distinct. However each arrangement would appear
objects were distinct. However each arrangement would appear
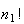 times as the
times as the
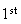 type was interchanged with itself,
type was interchanged with itself,
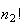 times as the
times as the
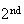 type was interchanged with itself, etc. Hence only
type was interchanged with itself, etc. Hence only
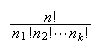 of the
of the
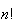 arrangements are distinct.
arrangements are distinct.
Example: 5 men and 3 women sit together in a row. Find the
probability that
-
the same gender is at each end
-
the women all sit together.
What are you assuming in your solution? Is it likely to be valid in real
life?
Solution: If we treat the people as being 8 objects --
5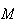 and
3
and
3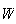 ,
our sample space will have
,
our sample space will have
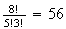 points.
points.
-
To get the same gender at each end we need either
 OR
OR
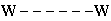
The number of distinct arrangements with a man at each end is
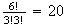 ,
since we are arranging
,
since we are arranging
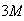 's
and
's
and
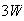 's
in the middle 6 positions. The number with a woman at each end is
's
in the middle 6 positions. The number with a woman at each end is
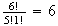 .
Thus
.
Thus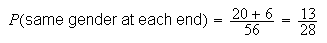 assuming each arrangement is equally likely.
assuming each arrangement is equally likely.
-
Treating
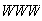 as a single unit, we are arranging 6 objects --
5
as a single unit, we are arranging 6 objects --
5 's
and 1
's
and 1
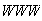 .
There are
.
There are
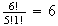 arrangements. Thus,
arrangements. Thus,
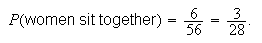
Our solution is based on the assumption that all points in
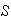 are equally probable. This would mean the people sit in a purely random order.
In real life this isn't likely, for example, since friends are more likely to
sit together.
are equally probable. This would mean the people sit in a purely random order.
In real life this isn't likely, for example, since friends are more likely to
sit together.
Problems:
-
Digits 1, 2, 3, ..., 7 are arranged at random to form a 7 digit number. Find
the probability that
-
the even digits occur together, in any order
-
the digits at the 2 ends are both even or both odd.
-
The letters of the word EXCELLENT are arranged in a random order. Find the
probability that
-
the same letter occurs at each end.
-
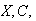 and
and
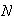 occur together, in any order.
occur together, in any order.
-
the letters occur in alphabetical order.
Combinations
This deals with cases where order does not matter; objects are drawn without
replacement.
The number of ways to choose
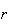 objects from
objects from
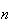 is denoted by
is denoted by
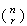 (called
"
(called
"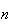 choose
choose
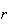 ").
For
").
For
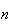 and
and
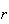 both non-negative integers with
both non-negative integers with
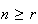 ,
,
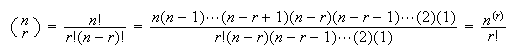
Proof: From result 2 earlier, the number of ways to
choose
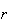 objects from
objects from
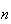 and arrange them from left to right is
and arrange them from left to right is
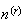 .
Any choice of
.
Any choice of
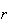 objects can be arranged in
objects can be arranged in
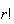 ways, so we must have
ways, so we must have
(Number of way to choose
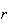 objects from
objects from
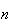 )
)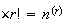
This gives
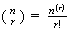 as the number of ways to choose
as the number of ways to choose
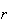 objects.
objects.
Note
that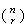 loses its physical meaning when
loses its physical meaning when
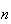 is not a non-negative integer
is not a non-negative integer
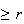 .
However it is defined mathematically, provided
.
However it is defined mathematically, provided
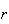 is a non-negative integer, by
is a non-negative integer, by
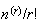 .
.
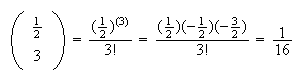
Example: In the Lotto 6/49 lottery, six numbers are drawn
at random, without replacement, from the numbers 1 to 49. Find the probability
that
-
the numbers drawn are 1, 2, 3, 4, 5, 6 (in some order)
-
no even number is drawn.
Solution:
-
Let the sample space
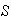 consist of all combinations of 6 numbers from 1, ..., 49; there are
consist of all combinations of 6 numbers from 1, ..., 49; there are
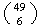 of them. Since 1, 2, 3, 4, 5, 6 consist of one of these 6-tuples,
of them. Since 1, 2, 3, 4, 5, 6 consist of one of these 6-tuples,
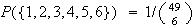 ,
which equals about 1 in 13.9 million.
,
which equals about 1 in 13.9 million.
-
There are 25 odd and 24 even numbers, so there are
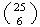 choices in which all the numbers are odd.
choices in which all the numbers are odd.
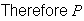 (no even number)
(no even number) |
= |
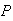 (all odd numbers)
(all odd numbers) |
|
= |
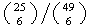 |
which is approximately equal to 0.0127.
Example: Find the probability a bridge hand (13 cards
picked at random from a standard deck) has
-
3 aces
-
at least 1 ace
-
6 spades, 4 hearts, 2 diamonds, 1 club
-
a 6-4-2-1 split between the 4 suits
-
a 5-4-2-2 split.
Solution: Since order of selection does not matter, we
take
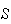 to have
to have
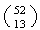 points.
points.
-
We can choose 3 aces in
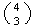 ways. We also have to choose 10 other cards from the 48 non-aces. This can be
done in
ways. We also have to choose 10 other cards from the 48 non-aces. This can be
done in
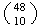 ways. Hence
ways. Hence
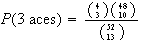
-
Solution 1: At least 1 ace means 1 ace or 2 aces or 3 aces or
4 aces. Calculate each part as in (a) and use the addition rule to get
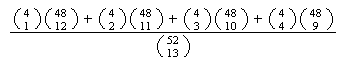
-
Solution 2: If we subtract all cases with
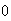 aces from the
aces from the
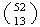 points in
points in
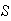 we are left with all points having at least 1 ace. This gives
we are left with all points having at least 1 ace. This gives
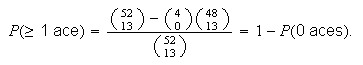 (The term
(The term
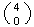 can be omitted since
can be omitted since
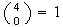 ,
but was included here to show that we were choosing
,
but was included here to show that we were choosing
 of the 4 aces.)
of the 4 aces.)
-
Solution 3: This solution is incorrect, but illustrates a common
error. Choose 1 of the 4 aces then any 12 of the remaining 51 cards.
This guarantees we have at least 1 ace, so
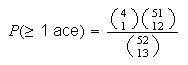
The flaw in this solution is that it counts some points more than once by
partially keeping track of order. For example, we could get the ace of spades
on the first choice and happen to get the ace of clubs in the last 12 draws.
We also could get the ace of clubs on the first draw and then get the ace of
spades in the last 12 draws. Though in both cases we have the same outcome,
they would be counted as 2 different outcomes.
(c)-
Choose the 6 spades in
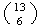 ways and the hearts in
ways and the hearts in
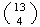 ways and the diamonds in
ways and the diamonds in
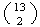 ways and the clubs in
ways and the clubs in
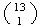 ways.
ways.
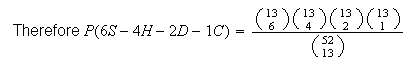
-
The split in (c) is only 1 of several possible 6-4-2-1 splits. In fact,
filling in the numbers 6, 4, 2 and 1 in the spaces above each suit
 defines a 6-4-2-1 split. There are 4! ways to do this, and then
defines a 6-4-2-1 split. There are 4! ways to do this, and then
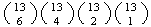 ways to pick the cards from these suits.
ways to pick the cards from these suits.
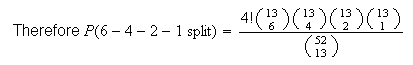
-
This is the same as (d) except the numbers 5-4-2-2 are not all different.
There are
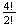 different arrangements of 5-4-2-2 in the spaces
different arrangements of 5-4-2-2 in the spaces
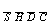 .
.
![$\bigskip$]()
Problems:
-
A factory parking lot has 160 cars in it, of which 35 have faulty emission
controls. An air quality inspector does spot checks on 8 cars on the lot.
-
Give an expression for the probability that at least 3 of these 8 cars will
have faulty emission controls.
-
What assumption does your answer to (a) require? How likely is it that this
assumption holds if the inspector hopes to catch as many cars with faulty
controls as possible?
-
In a race, the 15 runners are randomly assigned the numbers
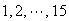 .
Find the probability that
.
Find the probability that
-
4 of the first 6 finishers have single digit numbers.
-
the fifth runner to finish is the 3rd finisher with a single digit number.
-
number 13 is the highest number among the first 7
finishers.0.2in
Problems on Chapter 3
-
Six digits from 2, 3, 4, ..., 8 are chosen and arranged in a row without
replacement. Find the probability that
-
the number is divisible by 2
-
the digits 2 and 3 appear consecutively in the proper order (i.e. 23)
-
digits 2 and 3 appear in the proper order but not consecutively.
-
Suppose
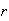 passengers get on an elevator at the basement floor. There are
passengers get on an elevator at the basement floor. There are
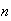 floors above (numbered 1, 2, 3, ...,
floors above (numbered 1, 2, 3, ...,
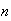 )
where passengers may get off.
)
where passengers may get off.
-
Find the probability
-
no passenger gets off at floor 1
-
passengers all get off at different floors
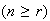 .
.
-
What assumption(s) underlies your answer to (a)? Comment briefly on how likely
it is that the assumption(s) is valid.
-
There are 6 stops left on a subway line and 4 passengers on a train. Assume
they are each equally likely to get off at any stop. What is the probability
-
they all get off at different stops?
-
2 get off at one stop and 2 at another stop?
-
Give an expression for the probability a bridge hand of 13 cards contains 2
aces, 4 face cards (Jack, Queen or King) and 7 others. You might investigate
the various permutations and combinations relating to card hands using the
Java applet at
-
The letters of the word STATISTICS are arranged in a random order. Find the
probability
-
they spell statistics
-
the same letter occurs at each end.
-
Three digits are chosen in order from 0, 1, 2, ..., 9. Find the probability
the digits are drawn in increasing order; (i.e., the first
 the second
the second
 the third) if
the third) if
-
draws are made without replacement
-
draws are made with replacement.
-
The Birthday Problem.
Note_1 Suppose there are
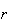 persons in a room. Ignoring February 29 and assuming that every person is
equally likely to have been born on any of the 365 other days in a year, find
the probability that no two persons in the room have the same birthday. Find
the numerical value of this probability for
persons in a room. Ignoring February 29 and assuming that every person is
equally likely to have been born on any of the 365 other days in a year, find
the probability that no two persons in the room have the same birthday. Find
the numerical value of this probability for
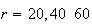 .
There is a graphic Java applet for illustrating the frequency of common
birthdays at http://www-stat.stanford.edu/%7Esusan/surprise/Birthday.html
.
There is a graphic Java applet for illustrating the frequency of common
birthdays at http://www-stat.stanford.edu/%7Esusan/surprise/Birthday.html
-
You have
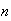 identical looking keys on a chain, and one opens your office door. If you try
the keys in random order then
identical looking keys on a chain, and one opens your office door. If you try
the keys in random order then
-
what is the probability the
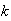 th
key opens the door?
th
key opens the door?
-
what is the probability one of the first two keys opens the door (assume
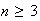 )?
)?
-
Determine numerical values for the answer in part (b) for the cases
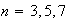 .
.
-
From a set of
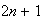 consecutively numbered tickets, three are selected at random without
replacement. Find the probability that the numbers of the tickets form an
arithmetic progression. [The order in which the tickets are selected
does not matter.]
consecutively numbered tickets, three are selected at random without
replacement. Find the probability that the numbers of the tickets form an
arithmetic progression. [The order in which the tickets are selected
does not matter.]
-
The 10,000 tickets for a lottery are numbered 0000 to 9999. A four-digit
winning number is drawn and a prize is paid on each ticket whose four-digit
number is any arrangement of the number drawn. For instance, if
winning number 0011 is drawn, prizes are paid on tickets numbered 0011, 0101,
0110, 1001, 1010, and 1100. A ticket costs $1 and each prize is $500.
-
What is the probability of winning a prize (i) with ticket number 7337? (ii)
with ticket number 7235? What advice would you give to someone buying a ticket
for this lottery?
-
Assuming that all tickets are sold, what is the probability that the operator
will lose money on the lottery?
-
-
There are 25 deer in a certain forested area, and 6 have been caught
temporarily and tagged. Some time later, 5 deer are caught. Find the
probability that 2 of them are tagged. (What assumption did you make to do
this?)
-
Suppose that the total number of deer in the area was unknown to you. Describe
how you could estimate the number of deer based on the information that 6 deer
were tagged earlier, and later when 5 deer are caught, 2 are found to be
tagged. What estimate do you get?
-
Lotto 6/49. In Lotto 6/49 you purchase a lottery ticket with
6 different numbers, selected from the set
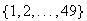 .
In the draw, six (different) numbers are randomly selected. Find the
probability that
.
In the draw, six (different) numbers are randomly selected. Find the
probability that
-
Your ticket has the 6 numbers which are drawn. (This means you win the main
Jackpot.)
-
Your ticket matches exactly 5 of the 6 numbers drawn.
-
Your ticket matches exactly 4 of the 6 numbers drawn.
-
Your ticket matches exactly 3 of the 6 numbers drawn.
-
(Texas Hold-em) Texas Hold-em is a poker game in which
players are each dealt two cards face down (called your hole or pocket cards),
from a standard deck of 52 cards, followed by a round of betting, and then
five cards are dealt face up on the table with various breaks to permit
players to bet the farm. These are communal cards that anyone can use in
combination with their two pocket cards to form a poker hand. Players can use
any five of the face-up cards and their two cards to form a five card poker
hand. Probability calculations for this game are not only required at the end,
but also at intermediate steps and are quite complicated so that usually
simulation is used to determine the odds that you will win given your current
information, so consider a simple example. Suppose we were dealt 2 Jacks in
the first round.
-
What is the probability that the next three cards (face up) include at least
one Jack?
-
Given that there was no Jack among these next three cards, what is the
probability that there is at least one among the last two cards dealt face-up?
-
What is the probability that the 5 face-up cards show two Jacks, given that I
have two in my pocket cards?
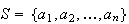 in which each simple event has probability
in which each simple event has probability
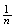 (i.e. is "equally likely"). Thus, if a compound event
(i.e. is "equally likely"). Thus, if a compound event
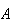 consists of
consists of
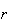 simple events, then
simple events, then
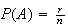 .
To use this approach we need to be able to count the number of events in
.
To use this approach we need to be able to count the number of events in
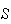 and in
and in
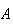 ,
and this can be tricky. We review here some basic ways to count outcomes from
"experiments". These approaches should be familiar from high school
mathematics.
,
and this can be tricky. We review here some basic ways to count outcomes from
"experiments". These approaches should be familiar from high school
mathematics.