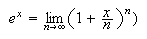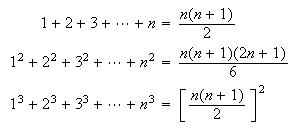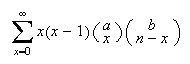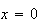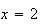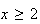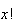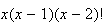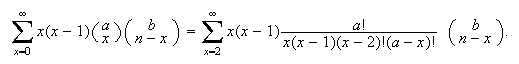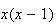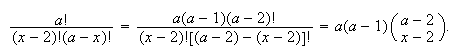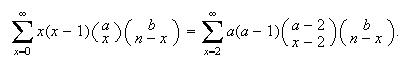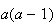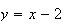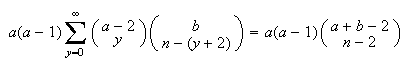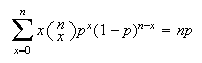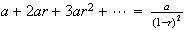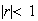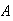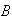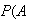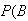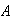5. Review of Useful Series and Sums
The preceding chapters have introduced ways to calculate the probabilities of
random events, based on various assumptions. You may have noticed that many of
the problems you've encountered are actually similar, despite the contexts
being different. Our approach in the next few chapters will be to classify
some of these common types of problems and develop general methods for
handling them. Rather than working each problem out as if we'd never seen one
like it before, our emphasis will now shift to checking whether the problem is
one of these general types.
Series and Sums
Before starting on the probability models of the next chapter, it's worth
reviewing some useful results for series, and for summing certain series
algebraically. We'll be making use of them in the next few chapters, and many,
such as the geometric series, have already been used.
-
Geometric Series: 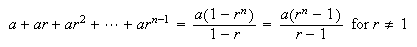 If
If 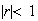 ,
then
,
then 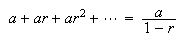
-
Binomial Theorem: There are various forms of this theorem.
We'll use the form 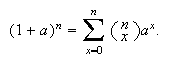 In a more general version, when
In a more general version, when 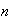 is not a positive integer,
is not a positive integer, 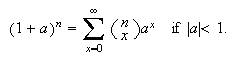 (We have already defined
(We have already defined 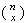 when
when 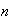 is not a positive integer.) While the binomial theorem may not look like
a summation result, we'll use it to evaluate series of the form
is not a positive integer.) While the binomial theorem may not look like
a summation result, we'll use it to evaluate series of the form 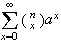 .
.
-
Multinomial Theorem: A generalization of the binomial
theorem is 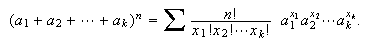 with the summation over all
with the summation over all 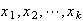 with
with 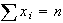 .
The case
.
The case 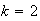 gives the binomial theorem in the form
gives the binomial theorem in the form 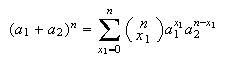 .
.
-
Hypergeometric Identity: 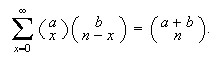 There will not be an infinite number of terms if a and b are positive integers
since the terms become 0 eventually. For example
There will not be an infinite number of terms if a and b are positive integers
since the terms become 0 eventually. For example 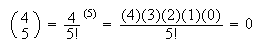
Sketch of Proof: 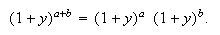 Expand each term by the binomial theorem and equate the coefficients of
Expand each term by the binomial theorem and equate the coefficients of
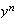 on each side.
on each side.
-
Exponential series: 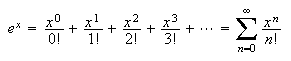 (Recall, also that
(Recall, also that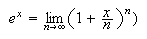
-
Special series involving integers: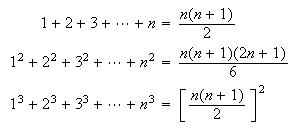
Example: Find
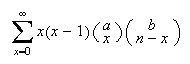
Solution: For
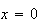 or 1 the term becomes 0, so we can start summing at
or 1 the term becomes 0, so we can start summing at
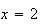 .
For
.
For
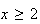 ,
we can expand
,
we can expand
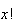 as
as
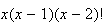
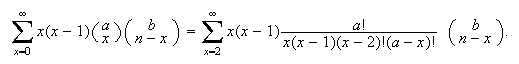 Cancel the
Cancel the
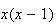 terms and try to re-group the factorial terms as "something choose something".
terms and try to re-group the factorial terms as "something choose something".
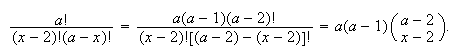 Then
Then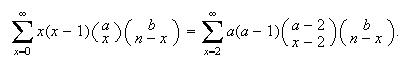 Factor out
Factor out
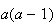 and let
and let
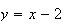 to
get
to
get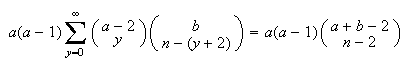 by the hypergeometric identity.
by the hypergeometric identity.
Problems on Chapter 5
(Solutions to 5.1 and 5.2
are given in Chapter 10.)
-
Show
that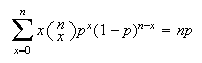 (use the binomial theorem).
(use the binomial theorem).
-
I have a quarter which turns up heads with probability 0.6, and a fair dime.
Both coins are tossed simultaneously and independently until at least one
shows heads. Find the probability that both the dime and the quarter show
heads at the same time.
-
Some other summation formulas can be obtained by differentiating the above
equations on both sides. Show that
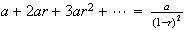 by starting with the geometric series formula. Assume
by starting with the geometric series formula. Assume
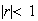 .
.
-
Players
 and
and
 decide to play chess until one of them wins. Assume games are independent with
decide to play chess until one of them wins. Assume games are independent with
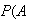 wins) = .3,
wins) = .3,
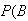 wins) = .25 and
wins) = .25 and
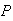 (draw)
= .45 on each game. If the game ends in a draw another game will be played.
Find the probability
(draw)
= .45 on each game. If the game ends in a draw another game will be played.
Find the probability
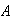 wins before
wins before
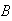 .
.
![]() If
If 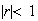 ,
then
,
then 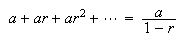
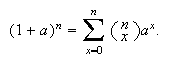 In a more general version, when
In a more general version, when 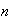 is not a positive integer,
is not a positive integer, 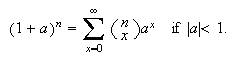 (We have already defined
(We have already defined 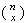 when
when 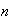 is not a positive integer.) While the binomial theorem may not look like
a summation result, we'll use it to evaluate series of the form
is not a positive integer.) While the binomial theorem may not look like
a summation result, we'll use it to evaluate series of the form 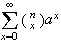 .
.
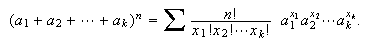 with the summation over all
with the summation over all  with
with  .
The case
.
The case 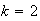 gives the binomial theorem in the form
gives the binomial theorem in the form 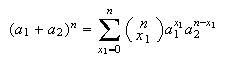 .
. 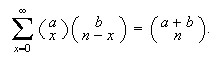 There will not be an infinite number of terms if a and b are positive integers
since the terms become 0 eventually. For example
There will not be an infinite number of terms if a and b are positive integers
since the terms become 0 eventually. For example 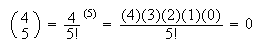
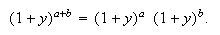 Expand each term by the binomial theorem and equate the coefficients of
Expand each term by the binomial theorem and equate the coefficients of
 on each side.
on each side. 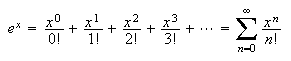 (Recall, also that
(Recall, also that