Probability


(Random House) a strong likelihood or chance of something. The relative possibility an event will occur ...the ratio of the number of actual occurrences to the total number of possible occurrences.
(equally probable outcomes) Let S=sample space (set of all possible distinct
outcomes). Then the probability of an event
=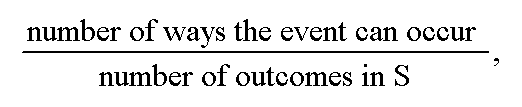
The probability of an event in an experiment is the proportion (or fraction) of times the event occurs in a very long (theoretically infinite) series of (independent) repetitions of experiment. (e.g. probability of heads=0.4992)
The probability of an event is a "best guess" by a person making the statement of the chances that the event will happen. (e.g. 30% chance of rain)
Definitions1 and 2 are consistent with one another if we are careful in constructing our model.
must be repeatable (at least in theory).
Has several possible distinct outcomes
A single repetition of the experiment is a ``trial''.
The probability of an event A, denoted P(A), is a number between 0 and 1.
(a) roll a fair die
(b) toss a fair coin until the first head appears
(c) Select a female student in Stat 230 and measure her height.
The set of all possible (indivisible) outcomes
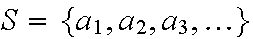 of a random experiment.
of a random experiment.
Above examples:
(a) S={1,2,3,4,5,6}
(b) S={H,TH,TTH,TTTH,...}
(c) S={x
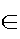 R;100
R;100
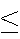 x
x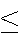 300 cm.}
300 cm.}
S has a finite or a countable number of points in it. (for example (a) and (b) above).
e.g. we write
S={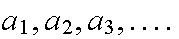 }
in this case. These "smallest" possible sets in S,
}
in this case. These "smallest" possible sets in S,
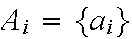 are simple events.
are simple events.
Consists of a sample space S and a
probability distribution (to be defined) defined on
S
Any subset of the sample space (in the case that S is discrete).
Let
S={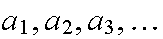 }
be a discrete sample space. Then probabilities
}
be a discrete sample space. Then probabilities
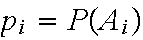 are numbers attached to the simple events
are numbers attached to the simple events
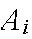 for
for
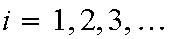 such that the following two conditions hold:
such that the following two conditions hold:
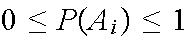
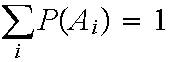
The set of values
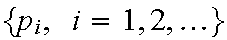 is called a probability distribution on
S.
is called a probability distribution on
S.
When the experiment is performed, some simple event in S must occur.
Definition: The probability P(A) of an general event A is the sum of the probabilities for all the simple events that make up A.
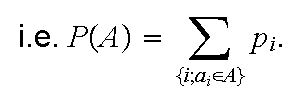
An event A made up of two or more simple events is
called a compound event.
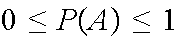 for any event A
for any event A
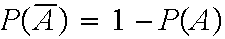 since
since
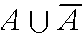 =S
=S
Example: Toss a fair coin until the first head appears.
S={H,TH,TTH,TTTH,...}. Then
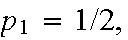
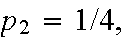
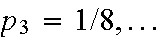 etc. The probability of A= "an even number of tosses
is
required"
etc. The probability of A= "an even number of tosses
is
required" 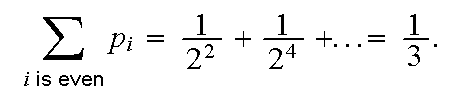 Probability
an odd number of tosses is required is
Probability
an odd number of tosses is required is
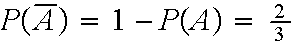 .
.
Example:
Toss a coin twice. Find the probability of getting 1 head.
Solution 1:
Let S={HH,HT,TH,TT} and assume the simple events each have probability 1/4. Then HT means head on the first toss and tails on the second. Since 1 head occurs for simple events HT and TH, A={HT,TH} we get P(1 head) =2/4=1/2.
Solution 2:
Let S = { 0 heads, 1 head, 2 heads } and assume the simple events each have probability 1/3. Then P(1 head) = 1/3.
Example:
Roll a red die and a green die. Find the probability the total is 6.
Solution:
Let (x,y) represent getting x
on the red die and y on the green die.
 All
points in S have probability 1/36.
All
points in S have probability 1/36.
A={(1,5),(2,4),(3,3),(4,2),(5,1)}
P(A)=5/36.
What if the dice are identical?
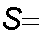 |
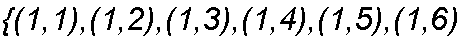 |
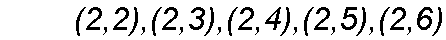 |
|
| ............... | |
 |
S has 21 points. P(A)=3/21?
What is the probability that a 5-card poker hand contains four of a kind?
(four twos or four threes, ...etc)
2.7 Machine Recognition of Handwritten Digits. An optical scanner determining which of the digits 0,1,...,9 an individual has written in a square box. The system may of course be wrong
Describe a sample space S that includes points (x,y), where x stands for the number actually written, and y stands for the number that the machine identifies.
Suppose that the machine is asked to identify very large numbers of digits, of which 0,1,...,9 occur equally often, and suppose that the following probabilities apply to the points in your sample space:
| p(0,6)=p(6,0)=.004; p(0,0)=p(6,6)=.096 |
| p(5,9)=p(9,5)=.005; p(5,5)=p(9,9)=.095 |
| p(4,7)=p(7,4)=.002; p(4,4)=p(7,7)=.098 |
| p(y,y)=0.100 for y=1,2,3,8 |
Give a table with probabilities for each point (x,y) in S. What fraction of numbers is correctly identified?

If sample space
S={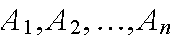 }
and each simple event has probability 1/n (i.e. is "equally likely"), then a
compound event A consisting of
r simple events, has probability
}
and each simple event has probability 1/n (i.e. is "equally likely"), then a
compound event A consisting of
r simple events, has probability
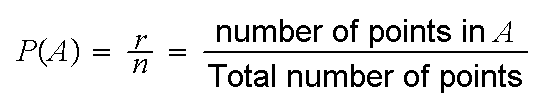
Example: Roll 3 fair dice. There are
6 6
6 6=216
possible outcomes, all equally likely. What is the probability of
A= "three dice are different numbers"? Number of
triples e.g. (1,2,3) with different numbers is
6
6=216
possible outcomes, all equally likely. What is the probability of
A= "three dice are different numbers"? Number of
triples e.g. (1,2,3) with different numbers is
6 5
5 4
so
4
so
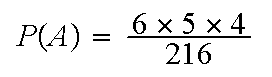
The Addition Rule:
Suppose we can either do job 1 in p ways or job 2 in
q ways. Then we can do either job 1
or job 2, (not both) in
p+q ways.
The Multiplication Rule:
Suppose we can do job 1 in p ways and an unrelated job
2 in q ways. Then we can do both job
1 and job 2 in
p q
ways.
q
ways.
n distinct objects are to be "drawn" or ordered from left to right (Order matters objects are drawn without replacement)
The number of ways to arrange n distinct objects in a
row is
n(n-1)(n-2) (2)(1)=n!
(2)(1)=n!
The number of ways to arrange r objects selected from
n distinct objects is
n(n-1)(n-2)...(n-r+1)=n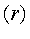
The number of ways to choose r objects from
n (a set, i.e. order doesn't matter) is denoted by
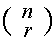 .
For n and r both non-negative
integers with
.
For n and r both non-negative
integers with
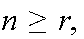
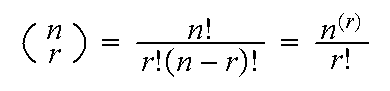
Example:
We form a 4 digit number by randomly selecting and arranging 4 digits from {1, 2, 3,…7} without replacement. Find the probability the number formed is (c) an even number over 3000.
S={1234,1235,...} has
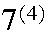 points.
points.
| Order filled | 2 | 3 | 4 | 1 |
| Number of choices | 5 | 5 | 4 | 1 (ends in 2) |
(5 5
5 4
4 1)
or
1)
or
| Order filled | 2 | 3 | 4 | 1 |
| Number of choices | 4 | 5 | 4 | 2 (ends in 4 or 6) |
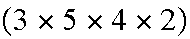
Total=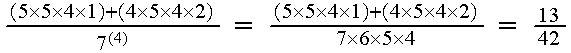
Beware of Double Counting!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Example: (p.26)
Find the probability a bridge hand (13 cards picked at random from a standard deck) has
3 aces
at least 1 ace
A1: P(hand has 1 ace or more) =
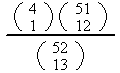 (is this correct?)
(is this correct?)
A2:
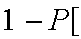 no
ace]
no
ace]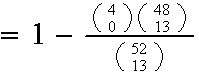
Suppose
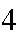 passengers get on an elevator at the basement floor. There are
passengers get on an elevator at the basement floor. There are
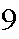 floors above (numbered
floors above (numbered
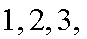 ...,
...,
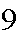 )
where passengers may get off.
)
where passengers may get off.
Find the probability
no passenger gets off at floor 1
A="passengers all get off at different floors"
B="all passengers get off at the same floor"
C="no-one gets of at the first two floors"
D="all passengers get off at floors 1 or nine"
G="exactly one person gets of at each of floors 3 and 4"
What assumption(s) underlies your answer to (a)? Comment briefly on how likely it is that the assumption(s) is valid.
e.g. S={1111,1112,...,9999} has
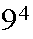 points. Of these
points. Of these
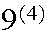 are such all passengers get off on different floors.
are such all passengers get off on different floors.
The Birthday Problem. Suppose there are
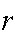 persons in a room. Ignoring February 29 and assuming that every person is
equally likely to have been born on any of the 365 other days in a year, find
the probability that no two persons in the room have the same birthday. Find
the numerical value of this probability
for
persons in a room. Ignoring February 29 and assuming that every person is
equally likely to have been born on any of the 365 other days in a year, find
the probability that no two persons in the room have the same birthday. Find
the numerical value of this probability
for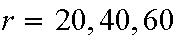 .
A:
.
A: 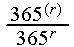 =0.411,0.891,0.994
http://www.ship.edu/%7Edeensl/mathdl/stats/Birthday.html
=0.411,0.891,0.994
http://www.ship.edu/%7Edeensl/mathdl/stats/Birthday.html
An event A "occurs" if one of the simple events in A occur.
e.g. throw a die, S={1,2,3,4,5,6}
A="Die is
even"={2,4,6}.
Union:
A B
means A OR B (or
possibly both)
occurs.
B
means A OR B (or
possibly both)
occurs.
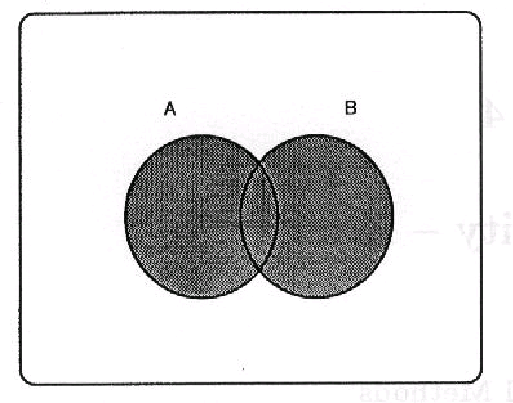
Intersection:
A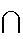 B
(usually written as AB in probability) is
shaded.
B
(usually written as AB in probability) is
shaded.
AB means A
and B both occur.
Complement:
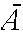 =points in S which are not in
A
=points in S which are not in
A
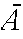 means "A does not occur"
means "A does not occur"

EXAMPLE SECTION 4.1: Students finishing 2A Math:
22% have a math average
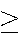 80%,
80%,
24% have a STAT 230 mark
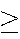 80%,
80%,
20% have an overall average
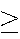 80%,
80%,
14% have both a math average and STAT 230
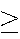 80%,
80%,
13% have both an overall average and STAT 230
 80%,
80%,
10% have all 3 of these averages
 80%,
80%,
67% have none of these 3 averages
 80%.
80%.
Find the probability a randomly chosen math student finishing 2A has math and
overall averages both
 80% and STAT 230
80% and STAT 230
 80%.
80%.
Events of interest.
| A | = | {Math
average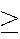 80%} 80%} |
|
| B | = | {Overall
average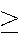 80%} 80%} |
|
| C | = | {Stat230
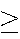 80%} 80%} |
Find __________________
Events
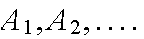 are mutually exclusive (disjoint) if, for all
are mutually exclusive (disjoint) if, for all
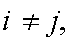
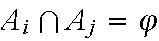 (the empty event)
(the empty event)
(at most one of these can ``happen'')
A probability measure is a set function
P( defined on subsets A of S
(i.e. assigning a real number value P(A) to subsets
A
defined on subsets A of S
(i.e. assigning a real number value P(A) to subsets
A such that:
such that:
P(S)=1
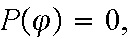
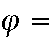 empty
event.
empty
event.
If
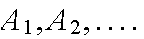 are mutually exclusive events, ( a finite number or an infinite
sequence)
are mutually exclusive events, ( a finite number or an infinite
sequence) 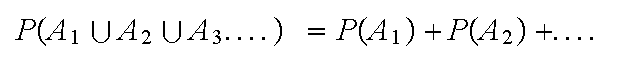
Other rules governing probability models:
For any event A,
0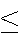 P(A)
P(A)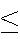 1
1
If A and B are two events with
A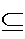 B,
then
P(A)
B,
then
P(A)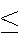 P(B).
P(B).
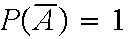 -P(A)
-P(A)
For any two events
A B
B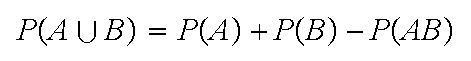
For any three events
A B
B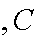
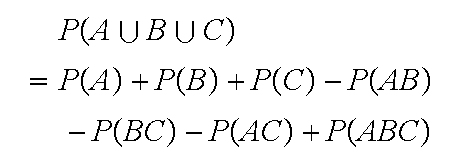
Example: Roll a die 3 times. Find the probability of getting at
least one 6.
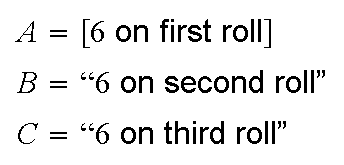 Then
Then
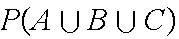 =P(A)+P(B)+P(C)=
=P(A)+P(B)+P(C)=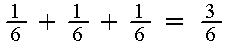 (it
this right?)
(it
this right?)
Example: A box contains 10 defective chips and 15 good ones. Twelve chips are drawn at random (without replacement). Find an expression for the probability that at most 5 defective chips are drawn.
Let
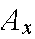 ="Exactly
x defective chips are
drawn".
="Exactly
x defective chips are
drawn".
Want
P(A)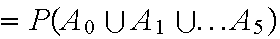 where
where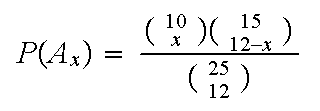 Then
P(A)
Then
P(A)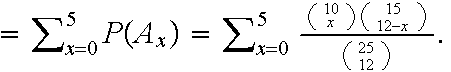
Intersection of Events and
Independence
Events A and B are
independent if
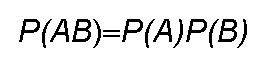
Indiana Jones: Raiders of the Lost Ark


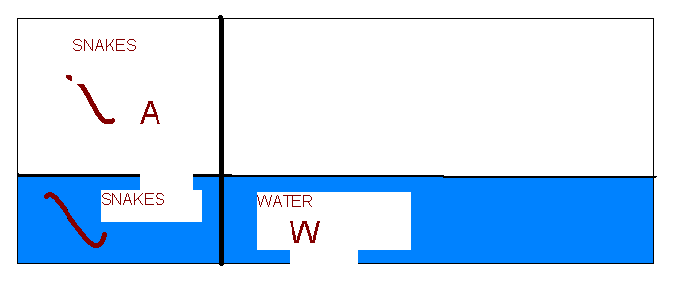
What is P(AW)?? P(A)=0.3, P(W)=0.4.
What is P(A\W) and when is it the same as
P(A)?
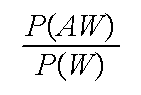
Definition: Events A and B
are independent if
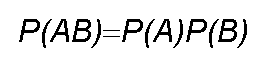
or if P(A\B)=P(A) where
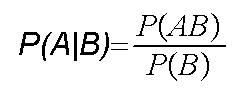 provided
denominator is greater than 0.
provided
denominator is greater than 0.
QUIZ UP TO & INCLUDING SECTION 4.3
Definition. Three or more events
A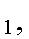 A
A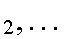 A
A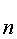 are mutually independent if for every choice of
are mutually independent if for every choice of
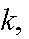
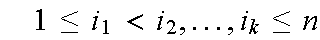
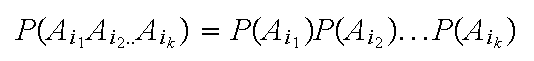
Example: Toss a die twice. Let A =
{first toss is a 3} and B = {the total is 7}. Are
A and B independent? Change
B to
B {total is 8}
{total is 8}
Why not call events independent if every pair of events is independent?
Two fair coins are tossed. Let
A first coin is heads, B = second coin is heads,
first coin is heads, B = second coin is heads,
 =
we obtain exactly one head. Then A is independent of
B and A is independent of
=
we obtain exactly one head. Then A is independent of
B and A is independent of
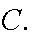 Are
A
Are
A B
B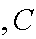 mutually
independent?
mutually
independent?
A B
independent implies
B
independent implies
A,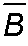 are independent,
are independent,
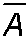 ,B
are independent
,B
are independent
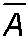 ,
,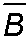 are independent
are independent
We are interested in the probability of the event
 A
A but we are given some relevant information, namely that another event
but we are given some relevant information, namely that another event
 B
B occurred.
occurred.
Revise the probabilities assigned to points of S in view of this new information. If the information does not effect the relative probability of points in B then the new probabilities of points outside of B should be set to 0 and those within B rescaled to add to 1.
For an event B with P(B)>0,
define the conditional probability
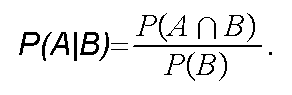 This
is another probability measure on the same sample space
S. Note that P(B\B)=1, and
P(
This
is another probability measure on the same sample space
S. Note that P(B\B)=1, and
P(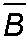 \B
\B =0.
=0.
Multiplication Rule: P(AB)=P(B)P(A\B)
Let A and B be events defined on the same sample space, with P(A)=0.3, P(B)=0.4 and P(A\B)=0.5. Given that event B does not occur, what is the probability of event A?
Three students Jane, Sue and Tom write an exam. Jane has a 90% chance of passing the exam, Sue has a 70% chance of passing and Tom has an 80% chance of passing. If exactly one of the students failed the exam, what is the probability it was Sue?

Note that we are given the event
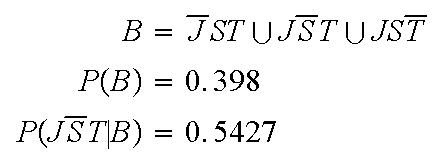
Let A,B,C,D be events in a sample space such that
A,AB,ABC
have positive probability.
Then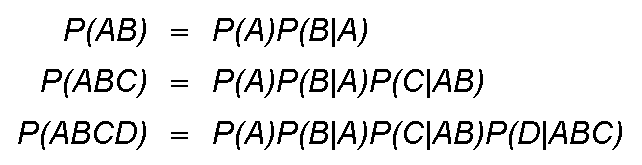
Let
 be a partition of the sample space S into disjoint
(mutually exclusive) events such that
be a partition of the sample space S into disjoint
(mutually exclusive) events such that
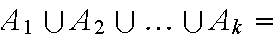 S.
Let B be an arbitrary event in
S. Then
S.
Let B be an arbitrary event in
S. Then
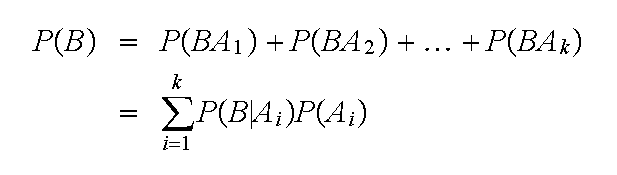
Many methods of spam detection are based on features that appear more
frequently in spam than in regular email. Conditional probability methods are
then used to decide whether an email is spam or not.
Define the following
events associated with a random email message.
| B | = | "Message is spam" |
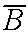 |
= | "Message is not spam |
| A | = | "Message contains the word Viagra" |
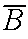 ),
then we can find the probabilities
P(B\A) and
P(
),
then we can find the probabilities
P(B\A) and
P(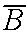 \A).
\A).
From a study of email messages coming into a certain system it is estimated
that P(B)=0.5,
P(A\B)=0.2, and
P(A\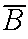 )=0.001.
Find
P(B\A
)=0.001.
Find
P(B\A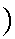 and
P(
and
P(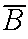 \A
\A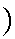 .
.
If you declared that any email containing the word Viagra was Spam, then find what fraction of regular (non-spam) emails would be incorrectly identified as Spam.
Review: "at least one of the events
A,B,C,D"=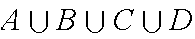
"all of the events A,B,C,D"=ABCD
"none of the events
A,B,C,D"=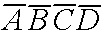
How do we calculate probabilities of the above?
Choosing appropriate Sample spaces: e.g. 3.8, 3.10, 3.11
Example (p. 48):
In an insurance portfolio 10% of the
policy holders are in Class
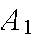 (high risk), 40% are in Class
(high risk), 40% are in Class
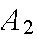 (medium risk), and 50% are in Class
(medium risk), and 50% are in Class
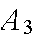 (low risk). The probability a Class
(low risk). The probability a Class
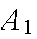 policy has a claim in a given year is .10; similar probabilities for Classes
policy has a claim in a given year is .10; similar probabilities for Classes
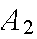 and
and
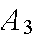 are .05 and .02. Find the probability that if a claim is made, it is for a
Class
are .05 and .02. Find the probability that if a claim is made, it is for a
Class
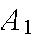 policy.
policy.
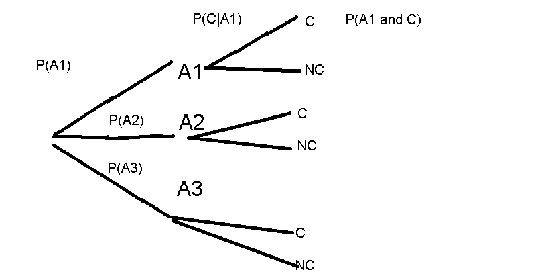
Tree- each path represents a sequence of events.
On a branch write the conditional probability of that event given preceding events
The probability at a node of the tree=product of probabilities on the branches leading to the node
= probability of the intersection of the events leading to it