The Model
SETS
LOCATIONS
ARCS
ALIAS(LOCATION,I,J)
- LOCATIONS:
represents all the nodes in the network problem, this includes Pedro’s Pizza and all the customers at the given time.
- ARCS:
represents all the arcs in the network problem. These arcs connect Pedro’s Pizza to each customer as well as each customer to each customer.
- ALIAS(LOCATION,I,J):
is used to rename the nodes in the network problem for easier reference. In this case, I and J will be used to reference the nodes.
DATA
DEMAND(I)
TABLE COST(I,J)
- DEMAND(I):
These values represent the supply and sink values for each node. Pedro’s pizza will thus have a negative value to represent supply which will be the number of pizzas ordered. The customers will have a positive value to represent
demand which will actually be the number of pizzas they require.
- TABLE COST(I,J):
These are the arc costs of the network problem. The arc cost will be a representational of the time and cost it takes to travel from node I to J. The values that have been assigned in the table incorporate various factors in
cluding, weather, time of day, traffic, traffic regulations and average travel times.
SCALARS
FIXED
ORDER
- FIXED
: this is a fixed cost incurred when a new delivery vehicle is introduced in the process of solving the problem.
- ORDER
: this is the current number of orders placed.
VARIABLES
X(I,I)
Y(I,I)
Z
- X(I,I):
this is a binary variable representing whether an arc is used or not. It has value 1 if the arc is used and 0 otherwise.
- Y(I,I):
this variable represents the number of pizzas the delivery vehicle is carrying on the trip from node I to J.
- Z:
this variable is the objective function value.
EQUATIONS
OBJ total time/cost to perform delivery
FLOW represents the flow conservation conditions. All customers' orders are fulfilled
MEET ensures only one driver will deliver to one customer
LEAVE ensures only one driver can leave a customer's location
BACK ensures the driver's return does not affect the delivery time
RESTRICT force variable to 0
OBJ: In the objective function, we are trying to minimize the costs and time to fulfill all customer orders.
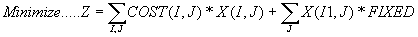
Cost of travelling from node I to J.  Each time a delivery vehicle is introduced a fixed cost is incurred.
Each time a delivery vehicle is introduced a fixed cost is incurred.
FLOW: These are the flow conservation conditions.

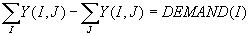
1) Supply of Pizza’s and demand of each customer.
2) Sum of the amount shipped in to node I.
3) Subtract the amount shipped out of node I
MEET: this ensures that only one delivery vehicle delivers to the customer. For example, if a customer requires 2 pizzas, then one vehicle will deliver to the customer, as opposed to 2 vehicles delivering 1 pizza each to the customer.
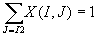
LEAVE: this constraint supplements the MEET constraint. Since only one delivery vehicle can deliver to a customer, than this constraint ensures only one delivery vehicle can leave the customer’s location.
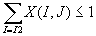
BACK: since we assumed that no driver returns to Pedro’s Pizza in order to complete his delivery, this constraint ensures this.
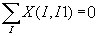
RESTRICT: this constraint ensures that if the arc is not used (i.e. X(I,J) = 0), then the delivery vehicle cannot carry any pizzas on this path (i.e. no amount can be shipped along the arc)
Y(I,J) <= ORDER*X(I,J)
To view the GAMS program that was formulated in the process of solving the problem, click here.
Click here to continue...
![]()
 Each time a delivery vehicle is introduced a fixed cost is incurred.
Each time a delivery vehicle is introduced a fixed cost is incurred.
![]()
![]()
![]()
![]()