


Next: About this document ...
Up: mid01
Previous: (20 points)
- Let
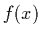 be twice continuously differentiable on
be twice continuously differentiable on 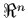 .
.
- Define local and global minimum for
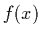 .
.
- Define Newton's method for minimization of
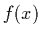 .
.
- Show that the function
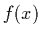 defined on
defined on 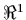 by
by
has a unique global minimizer at 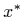 but that, for any nonzero initial
point
but that, for any nonzero initial
point 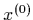 , the Newton's Method sequence
, the Newton's Method sequence
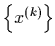 with
initial point
with
initial point 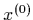 for minimizing
for minimizing 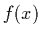 diverges.
diverges.
Henry Wolkowicz
2001-02-28
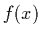 .
.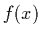 .
.