

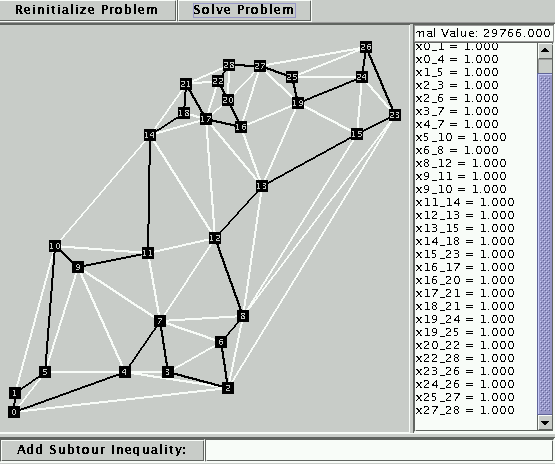
Finish: Done! The optimal LP solution is a tour! Since every tour is a potential LP solution, the tour found by the LP relaxation (being of minimum length among all LP solutions) must be an optimal tour.
The optimal tour length is 29,766 (you can read this value in the top right-hand-corner of the applet area, just above the window giving the values assigned to the edges).
It is not true that every example will have such a happy ending if we use only subtour-elimination constraints -- it is possible that the optimal LP value is less than the length of the optimal tour, even if all subtour-elimination constraints are satisfied.
In such a case, the cutting-plane method would proceed by adding other types of restrictions that are also satisfied by all tours.
It is an on-going research topic to find good classes of constraints for the TSP, along with methods to find violated constraints automatically from within computer codes.
| 



















