


Next: (10 points)
Up: mid01
Previous: mid01
- Define the following:
- convex set in
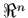
- convex function defined on
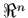
- closed convex cone in
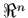
- dual (nonnegative polar) cone of a set
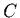 in
in 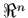
- Show that the following two sets are convex cones. Then
derive an explicit form for the dual (polar) cone
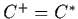 .
.
-
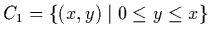 .
.
-
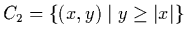 .
.
- Show that each of the above cones does not contain the point
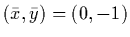 .
For each of the above cones find
a separating hyperplane with the point
.
For each of the above cones find
a separating hyperplane with the point
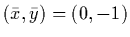 .
.
- Consider the quadratic objective function
- Find appropriate
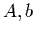 and write
and write
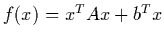 .
.
- Show that
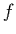 is a strictly convex function.
is a strictly convex function.
- Use the geometric characterization of optimality (Pshenichnyi
condition). Show that the origin in
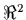 minimizes
minimizes 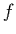 (defined
above) subject to
(defined
above) subject to 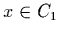 (defined in (2a) above).
(defined in (2a) above).
Henry Wolkowicz
2001-02-28
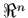
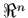
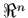
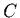 in
in 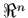
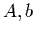 and write
and write
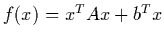 .
. 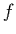 is a strictly convex function.
is a strictly convex function.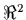 minimizes
minimizes 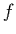 (defined
above) subject to
(defined
above) subject to 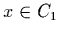 (defined in (2a) above).
(defined in (2a) above).