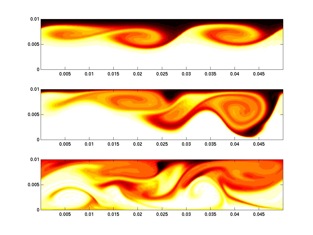
While many of the naturally occurring fluids we study are in a turbulent state all the time, the mathematical theory of fluid mechanics has traditionally not had much explicit to say about them.  Indeed, mathematics either provides general guiding principles (for example the fundamental absence in two dimensions of the vortex stretching mechanism that sustains turbulence) or deals with idealized solutions that are often simple.  On the mathematical side this says something about the limitations on the complexity of functions we can express as formulae.  On the physical side it points to the study of certain basic states of flow that are representative of fluid flow in general.  An example of such flows are one-dimensional shear flows.  In a lab these can be generated by taking a long tank filled with a density stratified fluid (think of a two-layer fluid with denser fluid under lighter fluid) and suddenly lifting one end of the tank.  The tilt causes the denser (lighter) fluid to flow downhill (uphill).  In the pictures from simulations above I show this basic flow with two green arrows in opposite directions.

 

The basic flow does not remain simple for long, and indeed a linear theory leading to an eigenvalue problem can be constructed to show this mathematically.  The simulations show how the disturbance evolves.  In the upper panel you can see three billows form as denser fluid is pulled over lighter fluid.  The billows interact and twist each other (middle panel) and a chaotic state eventually emerges (bottom panel).  Sometime around the time of the middle panel the flow begins to three-dimensionalize. The picture on the right shows a surface of constant density in shades of yellow and brown and regions of strong interaction with the top and bottom boundary in blue.