| Chapter 3: Induction and the Binomial Theorem |
|---|
One example of mathematical induction that is frequently used in computer science is recursion. Most programming languages allow the use of recursive functions or procedures.
A recursive routine is one that calls itself. It obviously must call itself with different arguments, otherwise it would enter an infinite loop. The routine evaluates itself with the new, usually smaller arguments, which would then call itself with different arguments again. This recursion continues until the routine reaches some base or stopping case. There may be one or more of these stopping cases.
For example, consider the function f (n) that is the sum of the first n integers. This can be defined in several different ways.
| Iteration: | f (n) | = | 1 + 2 + 3 + ... + n | |||
| Recursion: | f (n) | = | f (n - 1) + n | if n > 1; | and f (1) = 1 | |
| Closed form: | f (n) | = | n(n + 1) / 2 |
In a similar way the factorial function can be defined in two ways.
| Iteration: | n! | = | 1 . 2 . 3 . ... . n | |||
| Recursion: | n! | = | (n - 1)! . n | if n > 1; | and 0! = 1 |
The greatest common divisor of n integers can be defined recursively for n > 2 by
In this case the number of arguments change. The stopping case occurs when n = 2 ; we already know the value of GCD ( x1 , x2 ).
To prove that a recursive function produces the correct value, we usually have to use induction. We have to
is equal to n (n + 1) / 2 for n > 0.
Solution. (i) When n = 1, f (1) = 1 and also n ( n + 1 ) / 2 = 1; hence the result is true.
(ii) Assume, as induction hypothesis, that f (k) = k (k + 1) / 2, for some k > 0. Then
| f (k + 1) | = | f (k + 1) + k + 1 |
| = | k (k + 1) / 2 + (k + 1) | |
| = | (k + 1) (k + 2) / 2. |
| GCD ( a, b ) | = | | b | | if a = 0 | |
| GCD ( r , | a | ) | if a is not 0 |
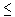r < | a |.
Using the computer science terminology for MOD, we have r = b MOD | a |. Hence the algorithm becomes
| GCD ( a, b ) | = | | b | | if a = 0 | |
| GCD ( b MOD | a | , | a | ) | if a is not 0 |
Compare this algorithm to Lemma 1.2.2, which was the basis for the standard Euclidean Algorithm 1.2.3.
For example,
| GCD ( -66, 39 ) | = | GCD ( 39, 66 ) | = | GCD ( 27, 39 ) | = | GCD ( 12, 27 ) |
| = | GCD ( 3, 12 ) | = | GCD ( 0, 3 ) | = | 3 |
In the above examples, the recursive function calls one copy of itself; this is called one-way recursion. It is also possible for the function to call multiple copies of itself. In two-way recursion the function calls two copies of itself. One example of this is the Quicksort Algorithm that is used to sort large lists, say to alphabetize a long list of words. This algorithm splits the list into two parts, and then applies the quicksort algorithm to both halves separately. These separately sorted halves then have to be merged together.