to the odd numbered Exercises and Problems in the Supplement
1. True statement
3. Not a statement
5. Not a statement
7.
9.
| P | Q | R | P => ( Q OR R ) |
T
T
T
T
F
F
F
F | T
T
F
F
T
T
F
F | T
F
T
F
T
F
T
F | T
T
T
F
T
T
T
T |
11.
| P | Q | R | ( P OR NOT Q ) => R |
T
T
T
T
F
F
F
F | T
T
F
F
T
T
F
F | T
F
T
F
T
F
T
F | T
F
T
F
T
T
T
F |
15.
| P | Q | P NOR Q |
T
T
F
F | T
F
T
F | F
F
F
T |
17. Q => P
19. P => Q
21. P <=> Q
25. P => Q
27. Q AND NOT P
29. If I have broken my leg then I cannot walk.
31. If I take the bus then I have broken my leg or I cannot walk.
33.  x
x  y x
y x 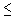 y ; integers
y ; integers
35.  x
x  y
y  z x > y z ; integers
z x > y z ; integers
37.  x ( NOT P(x) AND NOT Q(x) )
x ( NOT P(x) AND NOT Q(x) )
39.  x ( P(x) AND NOT Q(x) )
x ( P(x) AND NOT Q(x) )
41. Every real number is as large as any real number. False
43. There is a smallest real number. False
45. Equivalent
47. Not equivalent
49.  x ( ( x
x ( ( x A ) AND ( x
A ) AND ( x B ) AND ( x is not in C) )
B ) AND ( x is not in C) )
51. 
 >0
>0 
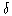 >0
>0  x ( 0 < | x - a | <
x ( 0 < | x - a | < 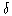 AND | f(x) - L |
AND | f(x) - L | 
 )
)
57. If x2 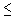 9 then x
9 then x 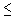 3.
3.
59. If a number is prime then it is not divisible by 2.
79. xn xn-1 ... x1 x1
81. x1 - 2 x2 + 4 x3 + ... + (-2)n-1 xn
83. e(0) = 1; e(n) = e(n - 1) + ( 1 / n! ) for n > 0
© 1998 William J. Gilbert and Scott A. Vanstone, University of Waterloo
Supplement Contents
 x
x  y x
y x 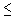 y ; integers
y ; integers
 x
x  y
y  z x > y z ; integers
z x > y z ; integers
 x ( NOT P(x) AND NOT Q(x) )
x ( NOT P(x) AND NOT Q(x) )
 x ( P(x) AND NOT Q(x) )
x ( P(x) AND NOT Q(x) )
 x ( ( x
x ( ( x A ) AND ( x
A ) AND ( x B ) AND ( x is not in C) )
B ) AND ( x is not in C) )

 >0
>0 
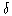 >0
>0  x ( 0 < | x - a | <
x ( 0 < | x - a | < 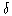 AND | f(x) - L |
AND | f(x) - L | 
 )
)
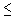 9 then x
9 then x 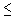 3.
3.