| |
(2.5) |
Consider the IVP
Definition 2.4.1 Let ![]() be an
eigenvalue of the
be an
eigenvalue of the
![]() matrix A of
multiplicity
matrix A of
multiplicity ![]() .
Then for
.
Then for
![]() ,
any non-zero solution v of
,
any non-zero solution v of
Exercise 2.4.1: Let v1 be a non-zero
solution of
Lemma 2.4.1: Let A be a real
![]() matrix with real eigenvalues
matrix with real eigenvalues
![]() repeated according to their
multiplicity. Then there exist n generalized
eigenvectors
repeated according to their
multiplicity. Then there exist n generalized
eigenvectors
![]() of
A, such that
of
A, such that
![]() is
nonsingular and A = S + N with
is
nonsingular and A = S + N with
Proof: (omitted)
Remark:
J = P-1 AP is called the
Jordan canonical form of A.
Theorem 2.4.1: Let A be a real
![]() matrix with real eigenvalues
matrix with real eigenvalues
![]() repeated according to their
multiplicity. Then the IVP (2.5) has a unique solution
given by
repeated according to their
multiplicity. Then the IVP (2.5) has a unique solution
given by
![\begin{displaymath}x(t) = P {\rm diag} \; [e^{\lambda_{j}t}] P^{-1} \left[ I
+ Nt +\cdots + \frac{N^{k}t^{k}}{k!} \right] x_{0} \, .
\end{displaymath}](img178.gif)
Corollary 2.4.1: If ![]() is a real
eigenvalue of multiplicity n of an
is a real
eigenvalue of multiplicity n of an
![]() matrix A, then
matrix A, then
![\begin{displaymath}x(t) = e^{\lambda t} \left[ I+Nt+ \cdots + \frac{N^{k}
t^{k}}{k!} \right] x_{0}
\end{displaymath}](img180.gif)
Example 2.4.1: Solve the IVP (2.5) with
![\begin{displaymath}A = \left[ \begin{array}{lrrr}
0 & -2 & -1 & -1 \\
1 & 2 & 1 & 1 \\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 1 \end{array} \right] \, .
\end{displaymath}](img181.gif)
Solution: It is easy to solve
![]() and find that A has an
eigenvalue
and find that A has an
eigenvalue
![]() of multiplicity 4. Thus
S=I
of multiplicity 4. Thus
S=I
![\begin{displaymath}N=A-S= \left[ \begin{array}{rrrr}
-1 & -2 & -1 & -1 \\
1 & 1 & 1 & 1 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 \end{array} \right]
\end{displaymath}](img184.gif)
![\begin{displaymath}N^{2} = \left[ \begin{array}{rrrr}
-1 & -1 & -1 & -1 \\
0 & ...
... & 0 \end{array} \right] \quad \mbox{and} \quad
N^{3} = 0 \, .
\end{displaymath}](img185.gif)
![\begin{eqnarray*}x(t) & = & e^{t} \left[ I+Nt+ \frac{N^{2}t^{2}}{2!} \right]
x_{...
...\frac{t^{2}}{2} \\
0 & 0 & 0 & 1 \end{array} \right] x_{0} \, .
\end{eqnarray*}](img186.gif)
In the general case, we must first determine a basis of
generalized eigenvectors for Rn and compute
![]() and N
= A - S.
and N
= A - S.
Example 2.4.2: Solve the IVP (2.5) with
![\begin{displaymath}A = \left[ \begin{array}{rll}
1 & 0 & 0 \\
-1 & 2 & 0 \\
1 & 1 & 2 \end{array} \right] \, .
\end{displaymath}](img188.gif)
Solution: A has eigenvalues
![]() ,
,
![]() .
It
is easy to find the corresponding eigenvectors
.
It
is easy to find the corresponding eigenvectors
![\begin{displaymath}v_{1} = \left[ \begin{array}{r}
1 \\ 1 \\ -2 \end{array} \rig...
..._{2} = \left[ \begin{array}{c}
0 \\ 0 \\ 1 \end{array} \right]
\end{displaymath}](img191.gif)
![$v_{3} = \left[ \begin{array}{c}
0 \\ 1 \\ 0 \end{array} \right]$](img193.gif) which is a solution of
which is a solution of
![\begin{displaymath}\left[ \begin{array}{rll}
-1 & 0 & 0 \\
-1 & 0 & 0 \\
1 & 1...
...= \left[ \begin{array}{c}
0 \\ 0 \\ 1 \end{array} \right] \, .
\end{displaymath}](img194.gif)
![\begin{displaymath}P = \left[ \begin{array}{rll}
1 & 0 & 0 \\
1 & 0 & 1 \\
-2 ...
... & 0 & 0 \\
2 & 0 & 1 \\
-1 & 1 & 0 \end{array} \right] \, .
\end{displaymath}](img195.gif)
![\begin{displaymath}S = P \left[ \begin{array}{lll}
1 & 0 & 0 \\
0 & 2 & 0 \\
0...
... & 0 & 0 \\
-1 & 2 & 0 \\
2 & 0 & 2 \end{array} \right] \, .
\end{displaymath}](img196.gif)
![\begin{displaymath}N = A -S = \left[ \begin{array}{rll}
0 & 0 & 0 \\
0 & 0 & 0 \\
-1 & 1 & 0 \end{array} \right] \, , \quad N^{2} = 0 \, .
\end{displaymath}](img197.gif)
![\begin{eqnarray*}x(t) & = & P \left[ \begin{array}{lll}
e^{t} & 0 & 0 \\
0 & e^...
...} + (2-t)e^{2t} & te^{2t} & e^{2t} \end{array}\right] x_{0} \, .
\end{eqnarray*}](img198.gif)
In case of multiple complex eigenvalues, we have the following Lemma whose proof can be found in Hirsch and Smale, Appendix III.
Lemma 2.4.2 Let A be
![]() matrix with complex eigenvalues
matrix with complex eigenvalues
![]() and
and
![]() ,
,
![]() ,
repeated according to their multiplicity. Then there
exist 2m generalized eigenvectors
wj =
uj + ivj and
,
repeated according to their multiplicity. Then there
exist 2m generalized eigenvectors
wj =
uj + ivj and
![]() ,
,
![]() such that
such that
![]() is nonsingular and
is nonsingular and
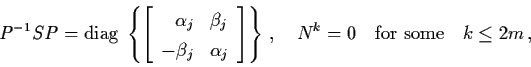
Remark:
J = P-1 AP is called the
Jordan canonical form of A.
Theorem 2.4.2: Under the assumptions of Lemma
2.4.2, the IVP (2.5) has a solution
![\begin{displaymath}x(t) = P {\rm diag} \; \left\{ e^{\alpha_{j}t} \left[
\begin{...
...t + \cdots + \frac{N^{k-1}
t^{k-1}}{(k-1)!} \right] x_{0} \, .
\end{displaymath}](img201.gif)
Example 2.4.3: Solve the IVP (2.5) with
![\begin{displaymath}A = \left[ \begin{array}{lrlr}
0 & -1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 0 & 0 & -1 \\
2 & 0 & 1 & 0 \end{array} \right] \, .
\end{displaymath}](img202.gif)
Solution: A has eigenvalues
![]() ,
,
![]() of multiplicity 2.
of multiplicity 2.
Solve (A-iI)w=0 and get the eigenvector
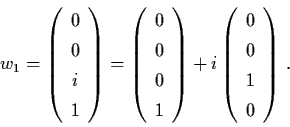
Solve
(A-iI) w = w1
to get the generalized eigenvector
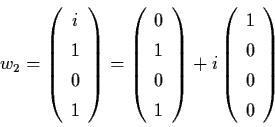
![\begin{displaymath}P = \left[ \begin{array}{cccc}
0 & 0 & 0 & 1 \\
0 & 0 & 1 & ...
... 1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \end{array} \right]
\end{displaymath}](img207.gif)
![\begin{displaymath}S = P \left[ \begin{array}{rlrl}
0 & 1 & 0 & 0 \\
-1 & 0 & 0...
...0 & 0 \\
0 & 1 & 0 & -1 \\
1 & 0 & 1 & 0 \end{array} \right]
\end{displaymath}](img208.gif)
![\begin{displaymath}N=A-S= \left[ \begin{array}{lrll}
0 & 0 & 0 & 0 \\
0 & 0 & 0...
... 0 \\
1 & 0 & 0 & 0 \end{array} \right] \, , \quad N^{2} = 0.
\end{displaymath}](img209.gif)
![\begin{eqnarray*}x(t) & = & P \left[ \begin{array}{rrrr}
\cos t & \sin t & 0 & 0...
...t \cos t & -t \sin t & \sin t & \cos t \end{array}\right] x_{0}.
\end{eqnarray*}](img210.gif)
In the general case, we have the following result. (Hirsch/Smale, P. 133)
Lemma 2.4.3 Let A be a real matrix
with real eigenvalues
![]() ,
,
![]() and complex eigenvalues
and complex eigenvalues
![]() ,
,
![]() ,
,
![]() ,
repeated according to their
multiplicity, where k+2m=n. Then there exist
generalized eigenvectors
,
repeated according to their
multiplicity, where k+2m=n. Then there exist
generalized eigenvectors
![]() ,
wk+1 = uk+1 + i vk+1,
,
wk+1 = uk+1 + i vk+1,
![]() ,
,
![]() ,
such
that the matrix
,
such
that the matrix
![$B_{j} = \left[ \begin{array}{rl}
\alpha_{j} & \beta_{j} \\
- \beta_{j} & \alpha_{j} \end{array} \right]$](img164.gif) ,
,
Remark: The matrix
J = P-1 AP is
called the Jordan canonical form of A.
Theorem 2.4.3: Under the assumption of Lemma
2.4.3 the IVP (2.5) has a solution
![\begin{displaymath}x(t) = P {\rm diag} \; \Biggl\{ e^{\lambda_{1}t} , \ldots ,
e...
...beta_{k+1}t & \cos \beta_{k+1}t \end{array}\right] , \ldots ,
\end{displaymath}](img166.gif)
![\begin{displaymath}e^{\alpha_{k+m} t} \left[ \begin{array}{rl}
\cos \beta_{k+m} ...
...t + \cdots +
\frac{N^{s-1} t^{s-1}}{(s-1)!} \right] x_{0} \, .
\end{displaymath}](img222.gif)
Based upon the above theorem, we arrive at the following important conclusion.
Theorem 2.4.4: Each coordinate in the solution
x(t) of the IVP (2.5) is a linear combination of
functions of the form