| |
(2.6) |
We shall discuss in this section the long term behaviour
of solutions of the linear system
It is easy to verify that the flow
![]() satisfies
satisfies
Definition 2.5.1: System (2.6) is called
From Theorem 2.4.4, we see that the following results hold.
Theorem 2.5.1: The origin is a sink of (2.6)
iff
![]()
Theorem 2.5.2: The origin is a source of
(2.6) iff
![]()
In general, let
![]() ,
be the eigenvalues of
A with multiplicity nj,
,
be the eigenvalues of
A with multiplicity nj,
![]() and
and
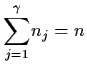 .
Then corresponding to each
.
Then corresponding to each
![]() ,
there are
mj linearly independent eigenvectors and
nj linearly independent generalized eigenvectors
with
,
there are
mj linearly independent eigenvectors and
nj linearly independent generalized eigenvectors
with
![]() .
mj is called the index
of
.
mj is called the index
of
![]() .
Clearly, A is diagonalizable
iff
mj = nj for all
.
Clearly, A is diagonalizable
iff
mj = nj for all
![]() .
It is easy to see that the real parts of
eigenvalues of A determine the asymptotic
behaviour of solutions of (2.6). Thus, we give the
following definition.
.
It is easy to see that the real parts of
eigenvalues of A determine the asymptotic
behaviour of solutions of (2.6). Thus, we give the
following definition.
Definition 2.5.2: Let
![]() ,
,
![]() ,
be the
eigenvalues of A repeated according to their
multiplicity and
wj = uj + i vj,
,
be the
eigenvalues of A repeated according to their
multiplicity and
wj = uj + i vj,
![]() ,
be the corresponding
generalized eigenvectors, where
,
be the corresponding
generalized eigenvectors, where
![]() and vj = 0 if
and vj = 0 if
![]() is a real eigenvalue. Then we define the
stable subspace Es, centre subspace Ec and unstable subspace Eu of (2.6) by
is a real eigenvalue. Then we define the
stable subspace Es, centre subspace Ec and unstable subspace Eu of (2.6) by
Clearly,
![]() ,
the origin is a sink when
Es = Rn, a source
when
Eu = Rn and a saddle when
,
the origin is a sink when
Es = Rn, a source
when
Eu = Rn and a saddle when
![]() .
.
From linear algebra, we know that a generalized
eigenspace of A, i.e. the span of generalized
eigenvectors corresponding to eigenvalues
![]() ,
is A-invariant, i.e.
,
is A-invariant, i.e.
![]() .
For the linear system (2.6), we have a similar concept.
.
For the linear system (2.6), we have a similar concept.
Definition 2.5.4: A subspace
![]() is said to be an invariant subspace of
(2.6) if
is said to be an invariant subspace of
(2.6) if
![]() for all
for all ![]() .
.
Theorem 2.5.3: The stable subspace
Es, center subspace Ec and unstable
subspace Eu are invariant subspaces of (2.6).
Proof: (omitted)
Thus for all ![]() ,
,
![]() and therefore
and therefore
![]() ,
i.e.
Es is invariant. Similarly, we can show that
Ec and Eu are invariant subspaces of
(2.6).
,
i.e.
Es is invariant. Similarly, we can show that
Ec and Eu are invariant subspaces of
(2.6).
Theorem 2.5.4: If the origin is a saddle point
of (2.6), then
![]() and
and
Example 2.5.1: Discuss the asymptotic
behaviour of solutions of (2.6) with
![\begin{displaymath}A = \left[ \begin{array}{rrl}
-2 & -1 & 0 \\
1 & -2 & 0 \\
0 & 0 & 3 \end{array} \right] \, .
\end{displaymath}](img265.gif)
Solution: A has eigenvalues
![]() ,
,
![]() and the
corresponding eigenvectors
and the
corresponding eigenvectors
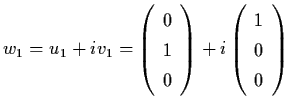 and
and
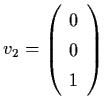 .
Then
.
Then
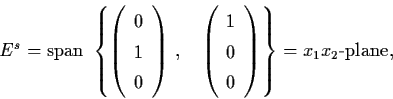
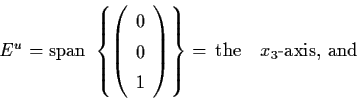
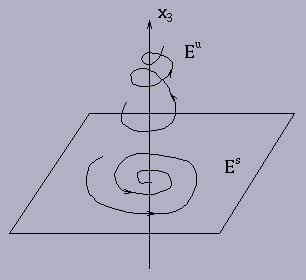
Example 2.5.2: Discuss the asymptotic
behaviour of solutions of (2.6) with
![\begin{displaymath}A = \left[ \begin{array}{lrl}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 2 \end{array} \right] \, .
\end{displaymath}](img272.gif)
Solution:
![]() ,
,
![]() ,
v1 = (0,0,1)T,
w1 = (0,1,0)T +i
(1,0,0)T.
,
v1 = (0,0,1)T,
w1 = (0,1,0)T +i
(1,0,0)T.
with period ![]() ,
i.e.
,
i.e.
![]() for all
for all ![]() .
In
general, solutions in Ec need not be bounded,
e.g.
.
In
general, solutions in Ec need not be bounded,
e.g.
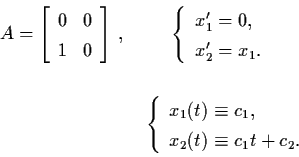
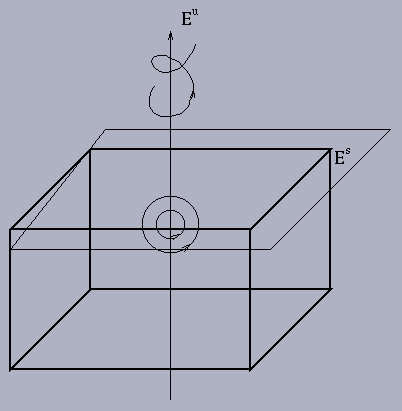
Since the flow eAt is determined by the eigenvalues and the generalized eigenspaces of A, many apparently different linear systems may have flows with identical asymptotic behaviour. Also for any k > 0, eAt and ekAt have the same phase portrait in the phase space Rn. Thus it is natural to classify all the linear systems by the following definition.
Definition 2.5.5: Two linear systems
x' =
A1 x and
x' = A2x in Rn are
said to be linearly equivalent if there exists k > 0
and a nonsingular matrix P such that
By this definition, all linear systems in Rn can be classified into a finite number of equivalent classes. For example, there are 14 equivalent classes in R2.
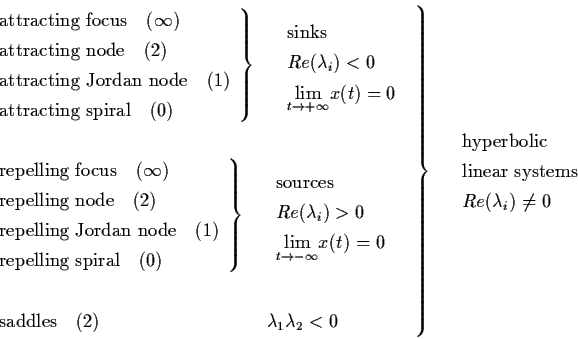
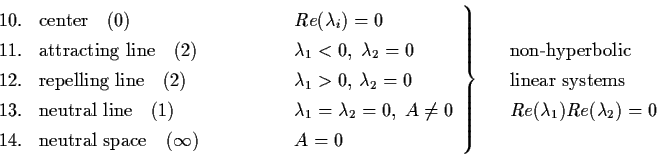
Note: The number or symbol in brackets ( ) is the
number of nontrivial invariant subspaces.