In this section, we consider the system
Theorem 2.6.1: If system (2.8) is a sink,
then there exists M, k > 0 such that
Proof: (omitted)
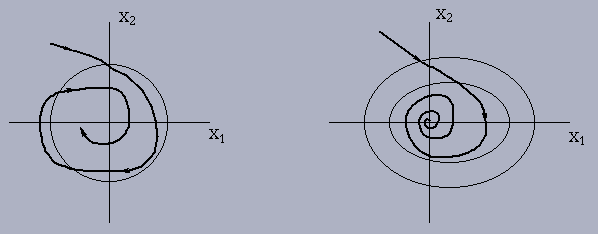
Although Theorem 2.6.1 guarantees that any initial state
is attracted at an exponential rate in time to a sink, it
does not imply that the distance from 0, i.e.
![]() decreases monotonically with
t. In other words as the orbits approach 0,
they do not necessarily cut the spheres
decreases monotonically with
t. In other words as the orbits approach 0,
they do not necessarily cut the spheres
![]() in the inward direction.
in the inward direction.
Theorem 2.6.2: If the origin is a sink of
(2.8), then there exists a positive definite matrix
Q such that
AT Q +QA = - I and the
quadratic function
Proof: (omitted)
Remark: In practice, to find Q one
usually solves the matrix equation (2.10) which is often
called the Lyapunov equation.
Example 2.6.1: Consider (2.8) with
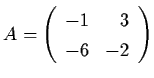 .
Then
AT Q +
QA = -I,
.
Then
AT Q +
QA = -I,
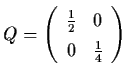 and
and
![]() .
.
Correspondingly, we have the following results for a source of (2.8).
Theorem 2.6.3: If the origin is a source of
(2.8), then
The proof is left as an exercise.