Theorem 3.1.1: Let
In this section, we consider the nonlinear systems of
ordinary differential equations
Theorem 3.1.1: Let ![]() be an
equilibrium point of (3.1) and suppose that all
eigenvalues of the matrix
be an
equilibrium point of (3.1) and suppose that all
eigenvalues of the matrix
![]() have
negative real parts. Then there exists a neighbourhood
U about
have
negative real parts. Then there exists a neighbourhood
U about ![]() such that for some
constant M, k > 0
such that for some
constant M, k > 0
We need the following Lemma whose proof can be found in the book by Hirsch/Smale, P. 145-9.
Lemma 3.1.1: Let A be an
![]() matrix and
matrix and
![]() for
all eigenvalues
for
all eigenvalues ![]() of A. Let
of A. Let
![]() be a basis for Rn. Then
for any
be a basis for Rn. Then
for any
![]() ,
,
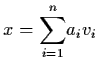 and
and
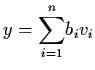 .
.
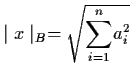 defines a norm in Rn and
defines a norm in Rn and
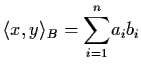 defines
an inner product in Rn.
defines
an inner product in Rn.
Proof of Theorem 3.1.1: (omitted)
Example 3.1.1: Consider the nonlinear oscillator (hard
spring)
![\begin{displaymath}y' = Df (0,0) y \,, \quad \mbox{where} \quad Df (0,0) =
\left...
...gin{array}{rr}
0 & 1 \\ -1 & - \alpha \end{array} \right] \, .
\end{displaymath}](img359.gif)
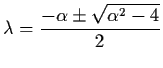 which have negative real parts. Thus by
Theorem 3.1.1, we conclude that there exists a
neighbourhood U , of the origin such that all solutions
(x1 (t),
x2(t)) of (3.3) starting in U satisfying
which have negative real parts. Thus by
Theorem 3.1.1, we conclude that there exists a
neighbourhood U , of the origin such that all solutions
(x1 (t),
x2(t)) of (3.3) starting in U satisfying
Naturally, we are interested in finding a neighbourhood
U of the origin in which all solutions of (3.3)
tend to (0,0) as
![]() .
By Theorem
2.6.2, we see that there exists a positive definite
matrix Q such that, letting
A = Df (0,0),
.
By Theorem
2.6.2, we see that there exists a positive definite
matrix Q such that, letting
A = Df (0,0),
![\begin{displaymath}Q = \left[ \begin{array}{ll}
\left( \frac{1}{\alpha} + \frac{...
...2} \\
\frac{1}{2} & \frac{1}{\alpha} \end{array} \right] \, .
\end{displaymath}](img364.gif)
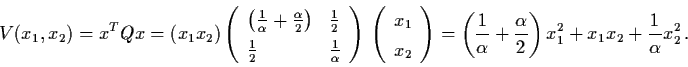
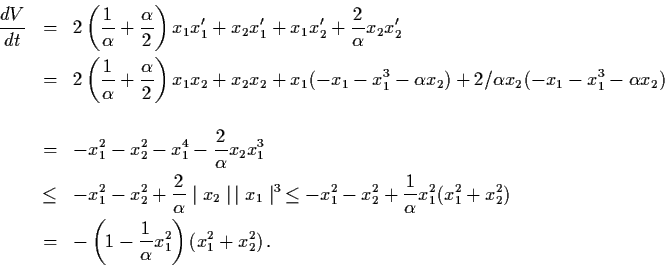
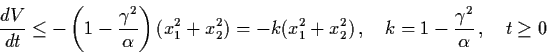
Thus
![]() ,
,
This example motivates the following result.
Theorem 3.1.2: Let ![]() be an
equilibrium point of the system (3.1) and suppose that
all eigenvalues of the matrix
be an
equilibrium point of the system (3.1) and suppose that
all eigenvalues of the matrix
![]() have
negative real parts. Then there exists a quadratic
function V(x) and a neighbourhood U about
have
negative real parts. Then there exists a quadratic
function V(x) and a neighbourhood U about
![]() such that
such that
![]() ,
V(x) = 0 iff
,
V(x) = 0 iff
![]() and
and
Proof: (omitted)
Theorem 3.1.3: Let ![]() be an
equilibrium point of the system (3.1) and suppose that
all eigenvalues of the matrix
be an
equilibrium point of the system (3.1) and suppose that
all eigenvalues of the matrix
![]() have
positive real parts. Then
have
positive real parts. Then
Theorems 3.1.1 - 3.1.3 tell us that solutions of the
nonlinear system (3.1) near the equilibrium point
![]() behave exactly as those of the corresponding
linear system at
behave exactly as those of the corresponding
linear system at ![]() .
Thus we give the following
definition.
.
Thus we give the following
definition.
Definition 3.1.1: Let ![]() be an
equilibrium point of (3.1). Then
be an
equilibrium point of (3.1). Then ![]() is called
is called
We will discuss solutions of (3.1) near a saddle point in section 3.4.