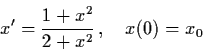3.2 Fundamental theory

In this section, we consider the nonlinear systems of ordinary differential equations

 

x' = f(x) (3.5)

where $x \in R^{n}$, $f : \Omega \raro R^{n}$ and $\Omega$ is an open subset of Rⁿ. Unlike linear systems with constant coefficients, it is not possible, in general, to solve the nonlinear system (3.5). However, we can show that under certain conditions on f, the nonlinear system (3.5) has a unique solution through each point $x_{0} \in \Omega$.

Theorem 3.2.1:     Let $\Omega$ be an open subset of Rⁿ and assume that $f \in C^{1} (\Omega )$. Then $\forall \quad x_{0} \in\Omega , \quad \exists \quad \alpha > 0$ such that the IVP

$$x' = f(x) \, , \quad x (0) = x_{0}$$ (3.6)

has a unique solution x(t) = x(t, x₀) on the interval $[ - \alpha , \alpha ]$.

Proof: (omitted)

Remark 1:     If the assumption f being C¹ is replaced by f being C⁰, the IVP (3.6) can still have existence which is guaranteed by Peano's theorem, but uniqueness may fail to hold. For example, the IVP $x' = 3x^{\frac{2}{3}}$, x(0) = 0 has solutions $x(t) \equiv 0$ and x (t) = t³, and in fact, it has infinitely many solutions. Note that $f(x) = 3x^{\frac{2}{3}}$ is continuous but not C¹. The following practical example is very interesting.

Example 3.2.1:     Leaky bucket problem

h(t) - water level (height) remaining in the bucket at time t.

A - area of the cross-section of the bucket,

a - area of the cross-section of the hole,

v(t) - velocity of the water leaving the hole.

Then

$$Ah' (t) = a v (t) \, .$$

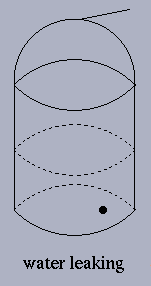
Assume no energy loss: $mgh = \frac{1}{2} mv^{2}$, $m = \Delta h A\rho$, $\rho$-density

v² = 2gh

$\Raro$      $Ah'(t) = -a \sqrt{2g} \, \sqrt{h}$, the minus sign indicates that h is decreasing in t.

$$h' = - c \sqrt{h} \, , \quad c = \frac{a \sqrt{2g}}{A} \, .$$

Q:     If at a given time, you see the bucket empty, can you figure out when it is (if ever) full?

$$\mbox{Initial value:} \qquad h(t_{0}) = 0 \, .$$

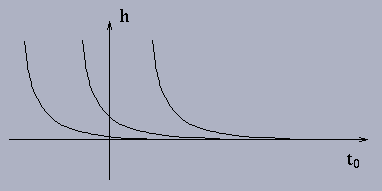
Clearly, the IVP

$$h' = - c \sqrt{h} \, , \qquad h (t_{0}) = 0$$

has more than one solution.

Remark 2:     From the proof of Theorem 3.2.1, we see that the condition f being C¹ can be replaced by f being Lipschitz, namely, there exists L > 0 such that

$$\mid f(t,x) - f (t,y) \mid \, \leq L \mid x-y \mid \, , \quad x, y \in D \, .$$

It is easy to see that if f has continuous partial derivatives, then f is Lipschitz on any compact subset of $\Omega$ but not conversely.

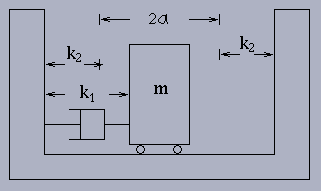
Example 3.2.2:     Consider a piecewise-linear oscillator shown below. (Dynamics & Stability of Systems, Vol. 6, P. 51, 1991)

The restoring force F_r is given by

$$F_{r} = \left\{ \begin{array}{l} - k_{1} x - k_{2} (x+ \alpha... ...{2} (x- \alpha ), \quad x \geq \alpha \, , \end{array} \right.$$

and the damping force $F_{\alpha} = - c x'$.

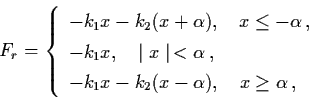
Thus the motion of the mass m is governed by

$$mx'' = - c x' + F_{r} (x) \, .$$

F_r is clearly Lipschitz but not C¹.

By Theorem 3.2.1, if $f \in C^{1} (\Omega )$, then $\forall \, x_{0} \in \Omega$ the IVP (3.6) admits a unique solution x(t) defined on $[ - \alpha , \alpha ]$ for some $\alpha > 0$. But the number $\alpha$ is, in general, very small. Thus Theorem 3.2.1 is often referred to local result. Naturally, we are interested in the existence of a solution x(t) of the IVP (3.6) defined on an interval as large as possible. This can be realized by extending the solution x(t) to both sides of the interval $[ - \alpha , \alpha ]$. The idea is as follows: since x(t) is defined on $[ - \alpha , \alpha ]$, the point $P_{0} = x(\alpha ) \in \Omega$. Then apply Theorem 3.2.1 to get an extension of x(t) on $[ - \alpha , \alpha + \alpha_{1}]$. $P_{1} = x(\alpha + \alpha_{1}) \in \Omega , \ldots ,$ continue. Extension to right proceeds $[- \alpha , \alpha + \alpha_{1} + \alpha_{2} + \cdots ]$. Similarly, proceed to left: $[ - \alpha - \beta_{1} - \beta_{2} - \cdots , \alpha ]$. The limits ${\dss\lim_{m \raro \infty}} (\alpha + \alpha_{1} + \alpha_{2} + \cdots + \alpha_{m}) = \beta^{*} \leq \infty$ and $P_{0}, P_{1}, \ldots , P_{m}, \ldots$, where P_m tends to the boundary of $\Omega$ as $m \raro \infty$. In general, we have the following definition.

Definition 3.2.1:     Let x(t) be a solution of the IVP (3.6) defined on an interval J. Then J is called a right-maximal interval of existence for x(t) if there does not exist an extension of x(t) over an interval J₁ so that x(t) remains a solution of the IVP (3.6) on J, and J is a proper subset of J₁ with different right endpoints. A left-maximal interval of existence for x(t) can be defined similarly. A maximal interval of existence for x(t) is an interval which is both a left-maximal and right-maximal interval.

The next theorem is an immediate consequence of the above discussion.

Theorem 3.2.2:     Let $\Omega$ be an open subset of Rⁿ and assume that $f \in C^{1} (\Omega )$ and let x(t) be a solution of the IVP (3.6) for $x_{0} \in \Omega$ on some interval. Then x(t) can be extended over a maximal interval of existence $(\alpha^{*}, \beta^{*})$. Moreover, if $(\alpha^{*}, \beta^{*})$ is a maximal interval of existence, then x(t) tends to the boundary of $\Omega$ as $t \raro \beta^{*}$ and $t \raro \alpha^{*}$.

Remark:     There is no guarantee that a solution x(t) to an IVP can be defined for all $t \in R$.

Example 3.2.3:     The IVP

$$x' = 1+x^{2}, \quad x(0) = x_{0}$$

has a solution $x(t) = \tan (t-c)$, $c = \tan^{-1} (x_{0})$. Such a solution cannot be extended beyond the interval $c - \frac{\pi}{2} < t < c + \frac{\pi}{2}$, since $x(t) \raro \pm \infty$ as $t \raro c \pm \frac{\pi}{2}$.

We usually say that such a solution has a ``finite escape time''.

The following corollaries of Theorem 3.2.2 are very useful in applications.

Corollary 3.2.1:     Let f(x) be continuously differentiable on Rⁿ and x(t) be a solution of (3.6) on a maximal right (left) interval J. Then either $J = [0, \infty )$ $(J = (- \infty , 0])$ or $J = [0, \beta^{*})$ $(J= (\alpha^{*}, 0])$ with $\beta^{*} < \infty$ $(\alpha^{*} > - \infty )$ and $\mid x(t) \mid \raro \infty$ at $t \raro \beta^{*} (\alpha^{*})$.

Corollary 3.2.2:     Let f(x) be continuously differentiable on Rⁿ and x(t) be a solution of (3.6) on a maximal interval J. Then $J = (- \infty , \infty )$ if one of the following is true:

(i)

x(t) is bounded on J,

(ii)

f(x) is bounded on Rⁿ.

Example 3.2.4:     Consider the hard spring again

   $$\left\{ \begin{array}{l} x'_{1} = x_{2}, \\ x'_{2} = - x_{1} - x_{1}^{3} - \alpha x_{2} \, .\end{array}\right.$$                                                    (3.8)

We are going to show that for any initial value $(x_{10}, \, x_{20}) \in R^{2}$, there is a unique solution (x₁(t), x₂(t)) of (3.8) existing on $[ 0, \infty )$. Clearly, the right-hand side of (3.8) is continuously differentiable on R². Let $V(x_{1}, x_{2}) = \frac{1}{2} x_{1}^{2} + \frac{1}{4} x_{1}^{4} + \frac{1}{2} x_{2}^{2}$. Then the derivative of V along solutions of (3.8) is

$$\frac{dV(x_{1}(t), x_{2}(t))}{dt} = x_{1} x'_{1} + x_{1}^{3} ... ...- x_{1}^{3} x_{2} - \alpha x_{2}^{2} = - \alpha x_{2}^{2} \, .$$

Thus V(x₁, x₂) is nonincreasing along any solution (x₁ (t), x₂(t)) of (3.8), i.e.

$$V(x_{1} (t), x_{2}(t)) \leq V (x_{10}, x_{20}), \quad t \geq 0$$

which implies that all solutions (x₁ (t), x₂(t)) of (3.8) are bounded on its right maximal interval of existence J. It follows by Corollary 3.2.2 that $J = [0, \infty )$.

Example 3.2.4 Simulation

Exercise 3.2.1:     Show that all solutions of the piecewise-linear oscillator considered in Example 3.2.2 are uniquely defined on $[ 0, \infty )$.

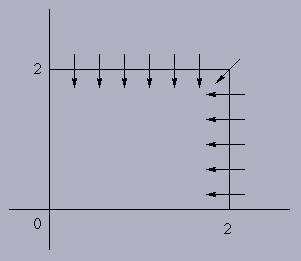
Example 3.2.5:     Consider the population growth model

$$\left\{ \begin{array}{l} x' = x - x^{2} - xy, \\ y = \frac{... ...} y - \frac{1}{4} y^{2} - \frac{3}{4} x y, \end{array} \right.$$ (3.9)

where x(t), y(t) represent species ``A'' and ``B'' at time $t \geq 0$. The population dynamics is being modeled as follows:

1.

1$^{\rm st}$ term ``x'' $({\rm \lq\lq }\frac{1}{2} y\mbox{''})$ represents the exponential growth which ``A'' (``B'') would experience in the presence of an unlimited food supply, with no internal competition or competition from ``B'' (``A'').

2.

2$^{\rm nd}$ term ``-x<sup>2</sup>'' $({\rm \lq\lq }- \frac{1}{4} y^{2}\mbox{''})$ models internal competition for food by 2 individuals of ``A'' (``B'').

3.

Last term represents competition between ``A'' and ``B'' for food.

Clearly, the right-hand side of (3.9) is of C¹ on R². From (3.9), one can see that for x,y > 0 sufficiently large (in fact x,y > 2 is sufficient) we have

$$\frac{dx}{dt} < 0 \quad \mbox{and} \quad \frac{dy}{dt} < 0 \, .$$

In other words, the vector field, hence solution curves, point inward toward the origin, as sketched below. Thus, as would be expected intuitively from the model, neither population, nor both, can go unchecked and increase without bound. Namely, all solutions of (3.8) are bounded and thus defined on $[ 0, \infty )$.

Example 3.2.5 Simulation

As you saw in Example 3.2.3 there are solutions that have ``finite escape time''. That is, a solution of a differential system is only defined on a finite interval. Intuitively, we may be able to eliminate this possibility by slowing down the motion, which is precisely the following result.

Theorem 3.2.3:     Let f(x) be C¹ (Rⁿ) and 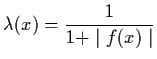$\lambda (x) = {\dss\frac{1}{1+ \mid f (x) \mid}}$. Then all solutions of the IVP

$$x' = \lambda (x) f(x) \, , \quad x(0) = x_{0}$$ (3.10)

are defined on R and have the same phase portraits as those of the IVP (3.6).

Proof: (omitted)

Remark:     The function $\lambda (x)$ can be chosen to be any positive function on Rⁿ. The idea is to rescale the vector field without changing its direction and consequently the orbits are unchanged. Intuitively, $\lambda (x)$ has the effect of ``slowing down'' the state point x, so that it cannot ``escape to infinity'' in a finite time.

Exercise 3.2.2:     Show that all solutions of the IVP

$$x' = \frac{1+x^{2}}{2+x^{2}} \, , \quad x (0) = x_{0}$$

are defined for all $t \in R$, and this DE has the same phase orbits as the one discussed in Example 3.2.3.