Definition 3.7.1: Let
We will introduce, in this section, an important concept called limit set, which is invariant. The invariant property of a limit set will enable us to weaken the conditions on asymptotic stability given in Theorem 3.5.1.
Consider the nonlinear system
Definition 3.7.1: Let
![]() and
and
![]() be the solution of
(3.29). Then a point
be the solution of
(3.29). Then a point
![]() is called an
is called an
![]() -limit (
-limit (![]() -limit) point x0 if
there exists a sequence
-limit) point x0 if
there exists a sequence
![]()
![]() ,
,
![]() as
as
![]()
![]() as
as
![]() )
such that
)
such that
By Definition 3.7.1, it is clear that if ![]() is
an asymptotically stable equilibrium, it is the
is
an asymptotically stable equilibrium, it is the
![]() -limit set of every point in its basin of
attraction. Any equilibrium is its own
-limit set of every point in its basin of
attraction. Any equilibrium is its own ![]() -limit set
and
-limit set
and
![]() -limit set. A closed orbit is the
-limit set. A closed orbit is the ![]() -limit
and
-limit
and ![]() -limit set of every point on it.
-limit set of every point on it.
Example 3.7.1: Consider the nonlinear system in
R2
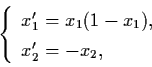
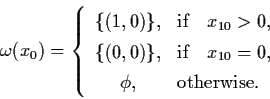
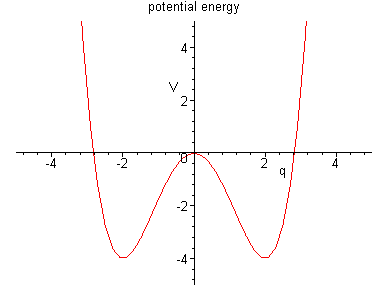
Example 3.7.2: Consider the magneto-elastic
beam. Let q denote the displacement of the tip of
the beam from the line of symmetry. Set, for simplicity,
the mass of the beam m=1. Then the force (elastic +magnetic) is
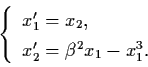
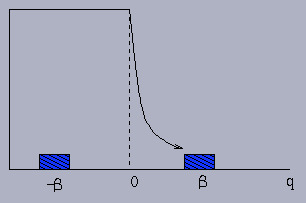
Let
x0 = (xi, 0), i=1,2,3, as shown. Then
we see
It should be noted that an ![]() -limit set
-limit set
![]() with respect to a flow
with respect to a flow
![]() is an
is an ![]() -limit set
-limit set
![]() with respect
to the flow
with respect
to the flow
![]() .
Thus we only need to
discuss the properties of
.
Thus we only need to
discuss the properties of ![]() -limit set. Clearly, the
long-term behaviour of the physical system whose evolution
is governed by (3.29) is described by the
-limit set. Clearly, the
long-term behaviour of the physical system whose evolution
is governed by (3.29) is described by the ![]() -limit
set
-limit
set
![]() of the given initial state
of the given initial state
![]() .
In order to determine the
.
In order to determine the
![]() -limit set, it is helpful to know a positively
invariant set since orbits entering a positively invariant
set never leave it, i.e. if E is invariant, then
-limit set, it is helpful to know a positively
invariant set since orbits entering a positively invariant
set never leave it, i.e. if E is invariant, then
![]() ,
,
![]() .
.
Theorem 3.7.1: Let
![]() and
and
![]() .
Then
.
Then
Proof: (omitted)
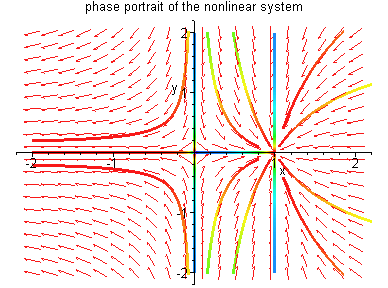
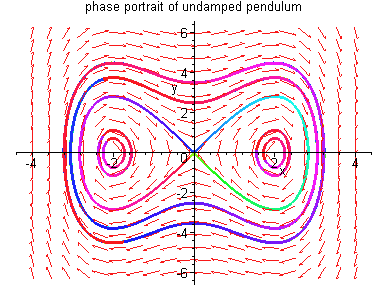
Here is a phase portrait of a nonlinear system to
illustrate the second possibility in the theorem.
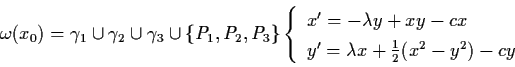
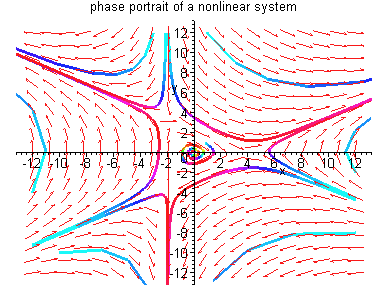
Corollary 3.7.1: If
![]() is a bounded and positively invariant set of (3.29),
then
is a bounded and positively invariant set of (3.29),
then
![]() ,
,
![]() and
and
![]() is invariant.
is invariant.
In order to determine the ![]() -limit sets, we again
resort to Lyapunov functions. The idea is that if
-limit sets, we again
resort to Lyapunov functions. The idea is that if
![]() for all
for all
![]() then V(x) will keep decreasing along
any solution
then V(x) will keep decreasing along
any solution
![]() staying in
staying in
![]() for all
for all ![]() until the solution
approaches its
until the solution
approaches its ![]() -limit set
-limit set
![]() .
Thus we expect
.
Thus we expect
![]() ,
which is a strong restriction on
the possible
,
which is a strong restriction on
the possible ![]() -limit sets. Based on this
observation and the invariance property of the limit set,
Barbashin and Krasovski generalized, in 1952, Lyapunov's
theorem (Th. 3.5.1) on asymptotic stability to the case
when the derivative of a Lyapunov function along solutions
of (3.29) is only semi-negative definite for periodic
differential equations. Inspired by their results, LaSalle
considered autonomous systems and made a number of
contributions. The general result is now known as
LaSalle's invariance principle.
-limit sets. Based on this
observation and the invariance property of the limit set,
Barbashin and Krasovski generalized, in 1952, Lyapunov's
theorem (Th. 3.5.1) on asymptotic stability to the case
when the derivative of a Lyapunov function along solutions
of (3.29) is only semi-negative definite for periodic
differential equations. Inspired by their results, LaSalle
considered autonomous systems and made a number of
contributions. The general result is now known as
LaSalle's invariance principle.
Theorem 3.7.2: Let
![]() ,
,
![]() ,
be continuously differentiable and
bounded from below . Assume that
,
be continuously differentiable and
bounded from below . Assume that
Proof: (omitted)
Since
![]() contains only whole orbits of
(3.29), the next result follows easily from Theorem 3.7.2
and Corollary 3.7.1.
contains only whole orbits of
(3.29), the next result follows easily from Theorem 3.7.2
and Corollary 3.7.1.
Corollary 3.7.2: Assume that
In view of Theorem 3.5.1 and Corollary 3.7.2, we obtain the following result which gives asymptotic stability under weaker conditions.
Theorem 3.7.3: Let ![]() be an
equilibrium point of (3.29),
be an
equilibrium point of (3.29),
![]() be an open set containing
be an open set containing ![]() and
and
![]() be continuously differentiable such that
be continuously differentiable such that
Example 3.7.3: Consider the nonlinear system
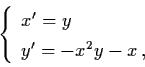
It should be noted that since the constant M is
arbitrary,
![]() as
as
![]() for any
for any
![]() ,
i.e. the domain of the attraction of (0,0) is R2. This is often called that (0,0)
is globally asymptotically stable.
,
i.e. the domain of the attraction of (0,0) is R2. This is often called that (0,0)
is globally asymptotically stable.
Example 3.7.4: Consider the predator prey system
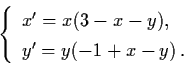
For x > 0 and y > 0, let
![]() .
Then V(x,y) >0 for x,y >
0 and
.
Then V(x,y) >0 for x,y >
0 and
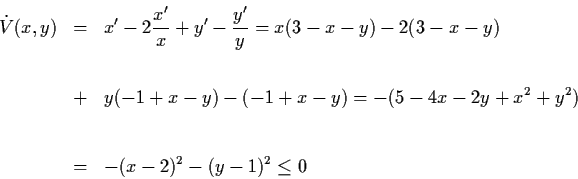
Example 3.7.5: Consider the damped
magneto-elastic beam
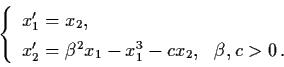
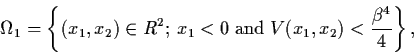
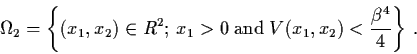
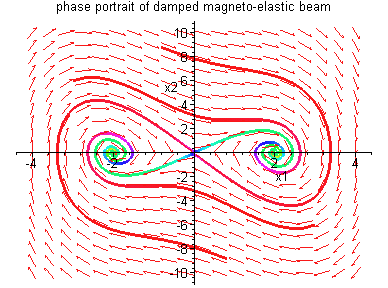
Remark: In applying the theorem, one must keep
in mind that the ![]() -limit set
-limit set
![]() is a whole orbit or the union of whole orbits. Thus one
has to find the whole orbits in the set
is a whole orbit or the union of whole orbits. Thus one
has to find the whole orbits in the set
![]() .
.
Example 3.7.6: Consider the damped pendulum
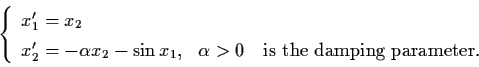
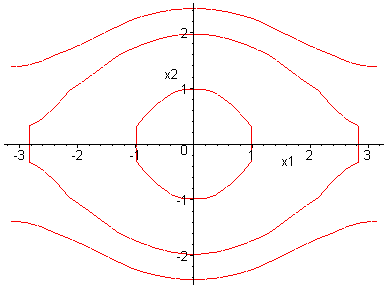
Clearly
![]() is
positive invariant. Thus
is
positive invariant. Thus
![]() ,
by Corollary 3.7.2
,
by Corollary 3.7.2
To conclude this section, it should be noted that although
the invariance property of the limit sets enables us to
weaken Lyapunov's theorem on asymptotic stability, the
structure of limit sets can be very complicated, and far
from being understood, e.g. the ``strange attractor'' for
the Lorenz system, see Perko,
P180-181. In fact, it
is still a very active area of current research especially
for higher
![]() dimensional systems. For two dimensional
systems, the limit sets are fairly simple and will be
discussed in depth in the next chapter.
dimensional systems. For two dimensional
systems, the limit sets are fairly simple and will be
discussed in depth in the next chapter.