| |
(3.25) |
In classical mechanics, free vibrations of a conservative
system can be described by
If we set p = q', then it is easy to see, from
(3.25) and (3.26), that
Let
![\begin{displaymath}x = {q \choose p} \, , \quad L = \left[ \begin{array}{rl}
0 & 1 \\ -1 & 0 \end{array}\right] \, .
\end{displaymath}](img663.gif)
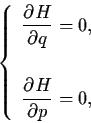
Thus is we take H as a Lyapunov function, then it
is easy to see, by Theorem 3.5.1, that the equilibrium
![]() is stable if the potential energy
function V(q) is positive definite with respect to
is stable if the potential energy
function V(q) is positive definite with respect to
![]() .
This establishes the famous Lagrange's
theorem. An equilibrium state
.
This establishes the famous Lagrange's
theorem. An equilibrium state
![]() is stable if the potential energy has local minimum at
is stable if the potential energy has local minimum at
![]() .
.
This is a result which is rather expected from physical intuition.
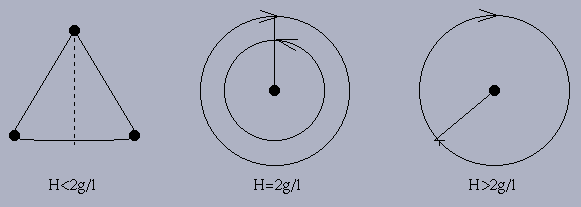
Example 3.6.1: Marble moving along landscapes
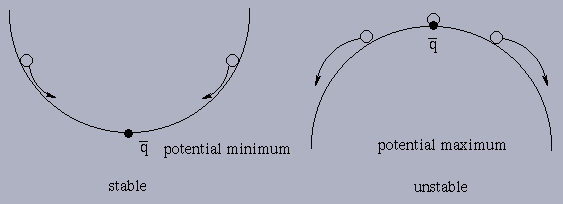
Marble rolling back and forth about ![]() .
.

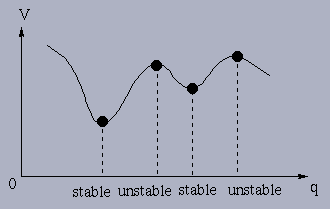
In general, the potential minima yield stable equilibria and maxima yield unstable (hyperbolic) equilibria. >
Example 3.6.2: Consider the mass-spring system
subject to a force
![]() ,
k >
0,
,
k >
0,
![]() .
.
Here
![]() corresponds to a ``hard'' spring,
i.e.,
corresponds to a ``hard'' spring,
i.e.,
![]() as
as
![]() ,
whereas
,
whereas
![]() corresponds to a ``soft''
spring, i.e. the restoring force becomes zero at
corresponds to a ``soft''
spring, i.e. the restoring force becomes zero at
![]() .
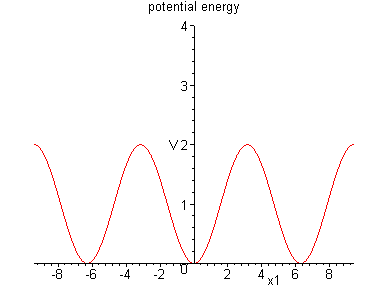
The potential energy is, for
general
.
The potential energy is, for
general ![]() ,
,
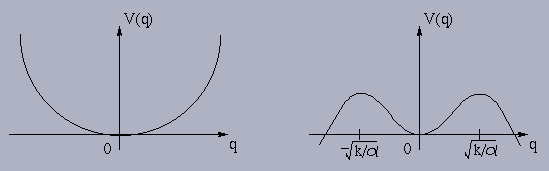
(0,0) is stable,
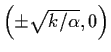 are unstable.
are unstable.
![]()

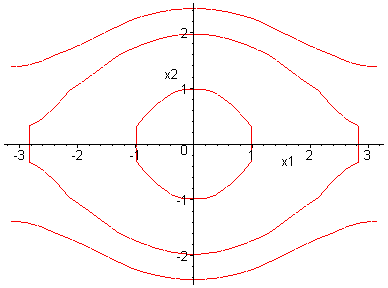
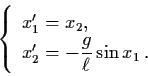
Thus
![]() are stable and
are stable and
![]() are unstable. A complete understanding of the phase
portraits for this problem is made possible with the
Hamiltonian function
are unstable. A complete understanding of the phase
portraits for this problem is made possible with the
Hamiltonian function
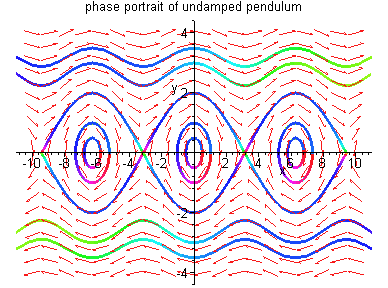
Note that periodic orbits have energies
![]() ,
orbits which travel from one unstable
equilibrium to another have energies
,
orbits which travel from one unstable
equilibrium to another have energies
![]() and trajectories with energy
and trajectories with energy
![]() move above or below the
x1-space. The trajectories connecting the saddle
points at
move above or below the
x1-space. The trajectories connecting the saddle
points at
![]() are called separatrices
since they separate regions of phase space with
qualitatively different dynamical behaviour.
are called separatrices
since they separate regions of phase space with
qualitatively different dynamical behaviour.
From the preceding discussion, you may guess that if the DE describes a physical system, then the choice of Hamiltonian or total energy as a Lyapunov function will always work. Unfortunately, this is somewhat incorrect, especially when we question what ``always work'' means. The following example should illustrate the idea.
Example 3.6.4: Consider the damped linear
oscillator
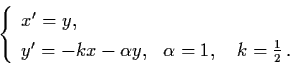
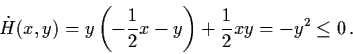
![$A = \left[
\begin{array}{rr}
0 & 1 \\ - \frac{1}{2} & -1 \end{array} \right]$](img692.gif) ,
,
The question arises: ``Can't we do better with the Lyapunov approach?''
The answer is ``yes'', only that we should choose a ``more suitable'' Lyapunov function. To ascertain what is ``more suitable'', we look at where the problem arose above.
The problem
![]() occurs only for y=0.
If we look at the picture below, we see that, on the line
y=0, the direction field,
occurs only for y=0.
If we look at the picture below, we see that, on the line
y=0, the direction field,
![]() ,
points only in the y direction, but
,
points only in the y direction, but
![]() points along the
x-axis for y =0. The problem then, lies in the fact
that the ellipses defined by level curves of
points along the
x-axis for y =0. The problem then, lies in the fact
that the ellipses defined by level curves of
![]() have their
principal axes lying along the x and y
axis.
have their
principal axes lying along the x and y
axis.
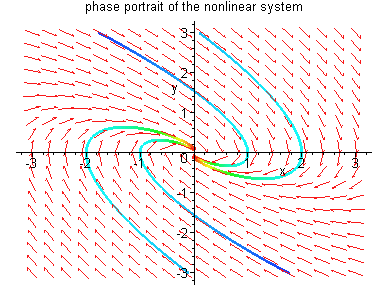
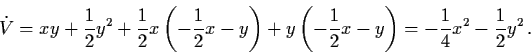
Remark: We conclude from the above example that
the mechanical energy function is not the best Lyapunov
function. Indeed, it was the energy function for
mechanical systems which inspired Lyapunov's stability
method. But the latter have exhibited much greater power
than the former method and it can be applied to very
general systems. Perhaps, the applicability of this method
today has gone beyond the imagination of Lyapunov himself.