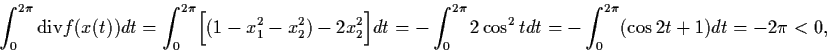4.1 Limit cycles and separatrix cycles

As is seen in Section 3.6, a Hamiltonian system can admit a family of periodic solutions which is dense in some closed set in Rⁿ. Of great interest is the case where a differential system admits an isolated periodic solution, i.e. the orbit has a neighbourhood which contains no other periodic orbits. This is, in fact, only possible for a nonlinear system. In this situation, the periodic solution may attract nearby solutions, thereby describing a physical system which has an oscillatory steady state.

Consider the nonlinear system

$$x' = f(x) \, .$$ (4.1)

Let $\phi_{t}(x_{0})$ be a periodic solution of (4.1). Then there exists a T > 0 such that $\phi_{t+T} (x_{0}) = \phi_{t} (x_{0})$, $\forall \; t \in R$. The minimal T for which this equality holds is called the period of the periodic solution $\phi_{t}(x_{0})$.

Example 4.1.1:     Consider the nonlinear system

$$\left\{ \begin{array}{l} x_{1}' = x_{2}, \\ x_{2}' = - x_{1} + (1 - x_{1}^{2} - x_{2}^{2}) x_{2}. \end{array}\right.$$ (4.2)

By inspection, we see that (4.1) admits a periodic solution

$$\gamma : \left\{ \begin{array}{l} x_{1} = \sin t, \\ x_{2} = \cos t, \quad t \in [0,2 \pi ] \, . \end{array}\right.$$

Let $V(x_{1}, x_{2}) = \frac{1}{2} (x_{1}^{2} + x_{2}^{2})$. Then

$$V' (x_{1}, x_{2}) = \nabla V (x) \cdot f (x) = x_{2}^{2} (1-x... ... & \mbox{if} & x_{1}^{2} + x_{2}^{2} < 1 , \end{array} \right.$$

which implies that any solution of (4.2) starting inside the unit circle will cut the concentric circles outward and those starting outside the unit circle will cut the concentric circles inward except at the points where x₂ = 0. But when x₂ = 0 and $x_{1} \neq 0$, $x_{2}' \neq 0$. Thus we conclude that the periodic orbit $\gamma$ attracts all other solutions except the origin, i.e. $\forall \; x_{0} \neq (0,0)$, $\omega (x_{0}) = \gamma$. This type of periodic solution is called a limit cycle. A formal definition is given below.

Example 4.1.1 Simulation

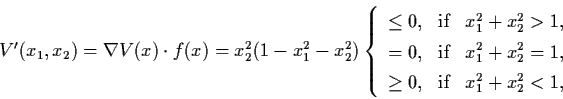
Definition 4.1.1:     An isolated periodic solution $\gamma$ of (4.1) is called a limit cycle if there exists a neighbourhood U of $\gamma$ such that $\omega (x_{0}) = \gamma$ for any $x_{0} \in U$.

In the study of periodic solutions in R², it is convenient sometimes to use polar coordinates. For instance, if we let $x_{1} = \rho \cos \theta$ and $x_{2} = \rho \sin \theta$ in Example 4.1.1, then system (4.2) reduces to

$$\left\{ \begin{array}{l} \rho' = (1-\rho^{2}) \rho \sin^{2} ... ...1 + (1-\rho^{2}) \sin \theta \cos \theta . \end{array} \right.$$ (4.3)

It is easy to see that system (4.3) admits a periodic solution

$$\gamma : \left\{ \begin{array}{l} \rho = 1, \\ \theta = - t, \quad 0 \leq t \leq 2 \pi \, . \end{array}\right.$$

Note that $\rho' > 0$ if $\rho < 1$ and $\theta \neq n \pi$ which implies that $\rho (t)$ is increasing.

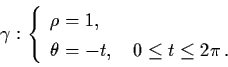
On the other hand, $\rho' < 0$ if $\rho > 1$ and $\theta \neq n \pi$, i.e. $\rho (t)$ is decreasing. This together with the fact $\theta' \neq 0$ when $\theta = n \pi$ implies that the periodic solution $\gamma$ attracts all other nonzero solutions.

Definition 4.1.2:     A periodic orbit $\gamma$ of (4.1) is called

(i)

stable if $\forall \; \veps > 0$, there exists a neighbourhood U of $\gamma$ such that $x_{0} \in U$ implies that $d(\phi_{t} (x_{0}), \gamma ) < \veps$, $t \geq 0$;

(ii)

asymptotically stable if (i) holds and there exists a neighbourhood U of $\gamma$ such that $\forall \; x_{0} \in U, \; d(\phi_{t}(x_{0}), \gamma ) \raro 0$ as $t \raro \infty$;

(iii)

unstable if (i) fails to hold.

Clearly, system (4.2) in Example 4.1.1 has a $2 \pi$-periodic solution which is asymptotically stable.

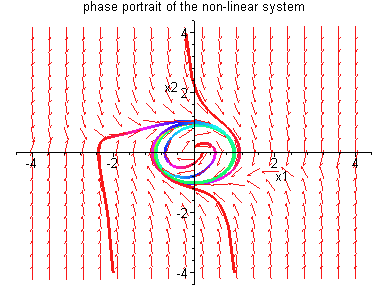
Example 4.1.2:     The system

$$\left\{ \begin{array}{l} x' = - y + x(1-x^{2}-y^{2}) \\ y' = x+y(1-x^{2} - y^{2}) \\ z' = z \end{array} \right.$$ (4.4)

has a periodic orbit in the xy-plane given by $(\cos t, \sin t, 0)$ which is unstable.

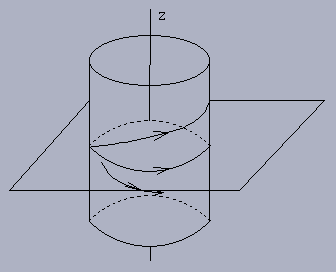
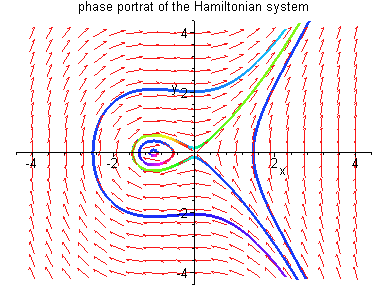
The next examples describe two important types of orbits that can occur in a dynamical system: homoclinic orbits and heteroclinic orbits.

Example 4.1.3:    Consider the Hamiltonian system

$$\left\{ \begin{array}{l} x' = y , \\ y' = x + x^{2} , \end{array} \right.$$ (4.5)

whose solution curves stay on the level sets of the Hamiltonian $H(x,y) = \frac{1}{2} y^{2} - \frac{x^{2}}{2} - \frac{x^{3}}{3}$, i.e.

$$y^{2} - x^{2} - \frac{2}{3} x^{3} = c.$$

The phase portraits of system (4.5) are shown on the right. The curve
y² = (x² + 2x³ /3), corresponding to, c=0, goes through the saddle point (0,0). The intersection of the stable and unstable manifolds is a closed curve containing an equilibrium point. This closed curve is called a separatrix cycle and the non-equilibrium solution curve on the separatrix cycle is called a homoclinic orbit.

Example 4.1.3 Simulation

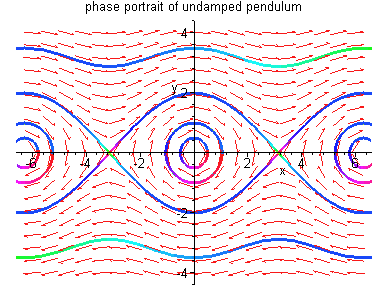
Example 4.1.4:     The following undamped pendulum

$$\left\{ \begin{array}{l} x_{1}' = x_{2}, \\ x_{2}' = -\sin x_{1} , \end{array} \right.$$ (4.6)

has phase portraits shown below.

The closed curve containing the equilibrium points $(- \pi , 0)$ and $(\pi , 0)$ defines a separatrix circle. The orbits connecting $(- \pi , 0)$ and $(\pi , 0)$ are called heteroclinic orbits.

Example 4.1.4 Simulation

To conclude this section, we state a theorem on stability of periodic solutions for 2-dimensional systems whose proof is omitted. See A.A. Andronov, et al., ``Theory of Bifurcations of Dynamical Systems on a Plane'', 1971.

Theorem 4.1.1:     Let $\Omega \subset R^{2}$ be an open set and $f \in C^{1} (\Omega )$. Let $\gamma : x(t)$, $0 \leq t \leq T$ be a periodic solution of (4.1) of period T. Then the periodic solution $\gamma$ is asymptotically stable if

$$\int_{0}^{T} {\rm div} f(x(t)) dt < 0$$

and it is unstable if

$$\int_{0}^{T} {\rm div} f(x(t)) dt > 0 \, .$$

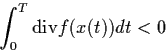
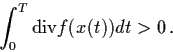
Example 4.1.5:     Consider the periodic solution $\gamma : \left\{ \begin{array}{l} x_{1} = \sin t, \\ x_{2} = \cos t, \quad t \in [0,2 \pi ] \end{array} \right.$ in Example 4.1.1. Since

$$\int_{0}^{2\pi} {\rm div} f(x(t)) dt = \int_{0}^{2\pi} \Bigl[... ...s^{2} t dt = - \int_{0}^{2\pi} (\cos 2t + 1) dt = - 2\pi < 0 ,$$

the periodic solution $\gamma$ is asymptotically stable.