Theorem 4.2.1: (Bendixson's Criterion) Let
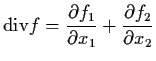 is nonzero and does not change sign on
is nonzero and does not change sign on
In this section, we consider the 2-dimensional system
Theorem 4.2.1: (Bendixson's Criterion) Let
![]() be a simply connected open set
and
be a simply connected open set
and
![]() .
If the divergence of the
vector field
.
If the divergence of the
vector field
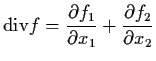 is nonzero and does not change sign on
is nonzero and does not change sign on
![]() ,
then the system (4.7) has no periodic orbit
lying entirely in
,
then the system (4.7) has no periodic orbit
lying entirely in ![]() .
.
Proof: (omitted)
Example 4.2.1: Consider the damped Hamiltonian
system in R2
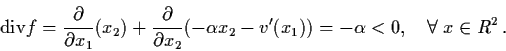
The following result due to Dulac is a generalization of Theorem 4.2.1.
Theorem 4.2.2: (Dulac's criterion) Let
![]() be a simply connected open set
and
be a simply connected open set
and
![]() .
If there exists a function
.
If there exists a function
![]() such that
such that
![]() is nonzero and does not change sign in
is nonzero and does not change sign in ![]() then (4.7) has no periodic orbits lying entirely in
then (4.7) has no periodic orbits lying entirely in
![]() .
.
Example 4.2.2: Consider the population growth
model
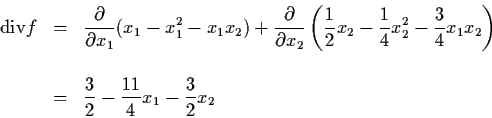
Let
B(x1, x2) = x1-1 x2-2. Then
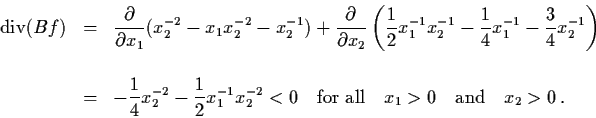
The next criterion for excluding periodic orbits, which is
valid in Rn, ![]() ,
is the Lyapunov
function approach.
,
is the Lyapunov
function approach.
Theorem 4.2.3: Let
![]() ,
where
,
where
![]() is an open set. If
is an open set. If
![]() ,
V(x) is bounded from below on
,
V(x) is bounded from below on ![]() ,
and the
set
,
and the
set
![]() contains no whole orbits except possibly equilibrium points
of (4.7), then the system (4.7) has no periodic
solutions lying entirely in
contains no whole orbits except possibly equilibrium points
of (4.7), then the system (4.7) has no periodic
solutions lying entirely in ![]() .
.
Proof: It follows from Theorem 3.7.2.
Example 4.2.3: Consider the nonlinear system