


Next: Maple Worksheet
Up: Periodic Solutions and Bifurcations
Previous: Structural stability and bifurcation
We discussed, in the last section, various types of
bifurcations that occur at an equilibrium point 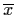 of the system
of the system
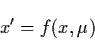 |
(4.38) |
when the matrix
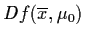 has a simple
zero eigenvalue. In this section, we consider bifurcations
that occur when the matrix
has a simple
zero eigenvalue. In this section, we consider bifurcations
that occur when the matrix
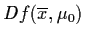 has
a simple pair of pure imaginary eigenvalues and no other
eigenvalues with zero real part. In this case, a Hopf
bifurcation can occur and a periodic orbit is created as
has
a simple pair of pure imaginary eigenvalues and no other
eigenvalues with zero real part. In this case, a Hopf
bifurcation can occur and a periodic orbit is created as
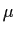 passes through the bifurcation value
passes through the bifurcation value
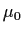 .
Let us first consider a simple example.
.
Let us first consider a simple example.
Example 4.6.1: Consider the two-dimensional
system
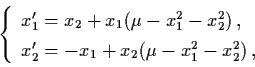 |
(4.39) |
where 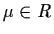 is a parameter.
is a parameter.
There is only one equilibrium point (0,0) and
Thus the origin is asymptotically stable if 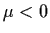 and unstable if
and unstable if 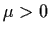 .
For
.
For 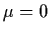 ,
Df
(0,0) has a pair of pure imaginary eigenvalues. The
structure of the phase portrait becomes apparent if we
rewrite system (4.39) in polar coordinates. Let
,
Df
(0,0) has a pair of pure imaginary eigenvalues. The
structure of the phase portrait becomes apparent if we
rewrite system (4.39) in polar coordinates. Let
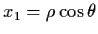 and
and
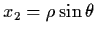 .
Then (4.39) reduces to
.
Then (4.39) reduces to
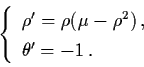 |
(4.40) |
We see from (4.40) that when
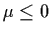 ,
the
origin is asymptotically stable and when
,
the
origin is asymptotically stable and when 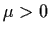 ,
the origin becomes unstable and there is a periodic orbit
,
the origin becomes unstable and there is a periodic orbit
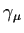 given by
given by
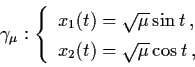 |
(4.41) |
which is asymptotically stable. Thus 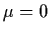 is a
bifurcation value. The phase portraits and bifurcation
diagram are shown below.
is a
bifurcation value. The phase portraits and bifurcation
diagram are shown below.
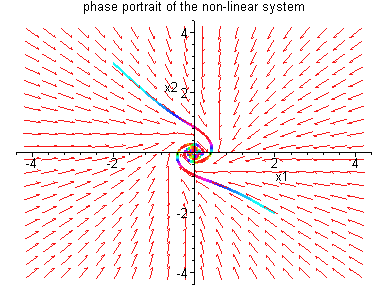
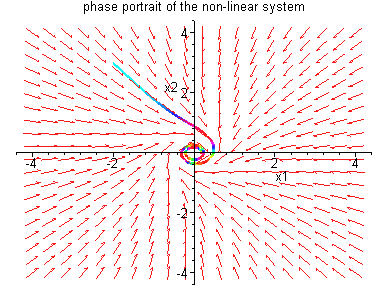
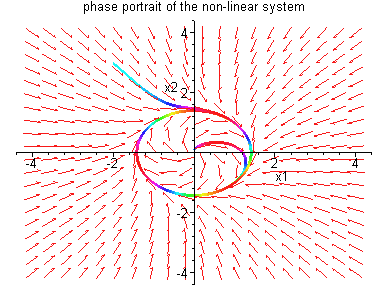
Figure 4.6.1: Phase portraits for system (4.39)
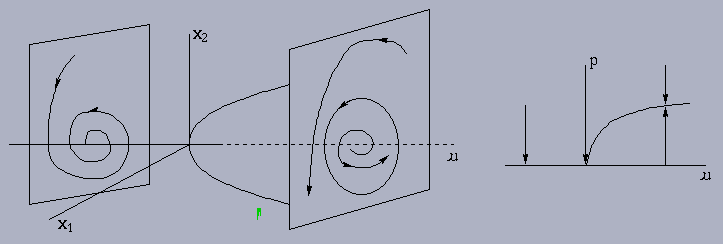
Figure 4.6.2: The bifurcation diagram
This type of bifurcation is called a Hopf bifurcation.
Next, we consider system (4.38) in R2 and
assume that it be written into the form
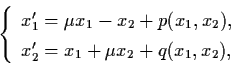 |
(4.42) |
where
Let
![\begin{displaymath}\sigma = \frac{3 \pi}{2} [3(a_{30} + b_{03}) + (a_{12} +
b_{2...
...02}) + a_{11}(a_{02}+
a_{20}) - b_{11} (b_{02} + b_{20})] \, .
\end{displaymath}](img1025.gif) |
(4.43) |
Then we have the following theorem (L. Perko, p. 317).
Theorem 4.6.1: (Hopf Bifurcation) If
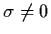 ,
then a Hopf bifurcation occurs at the
origin of system (4.42) at the bifurcation value
,
then a Hopf bifurcation occurs at the
origin of system (4.42) at the bifurcation value 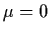 ;
in particular, if
;
in particular, if
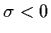 ,
then system
(4.42) has a one-parameter family of stable limit cycles
for
,
then system
(4.42) has a one-parameter family of stable limit cycles
for 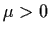 and no limit cycles for
and no limit cycles for
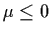 ,
and if
,
and if
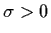 ,
then system (4.42) has
a one-parameter family of unstable limit cycles for
,
then system (4.42) has
a one-parameter family of unstable limit cycles for
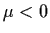 and no limit cycles for
and no limit cycles for
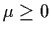 .
.



Next: Maple Worksheet
Up: Periodic Solutions and Bifurcations
Previous: Structural stability and bifurcation
![]() of the system
of the system
![\begin{displaymath}Df (0, \mu ) = \left[ \begin{array}{rc}
\mu & 1 \\ -1 & \mu \end{array} \right] \, .
\end{displaymath}](img1018.gif)




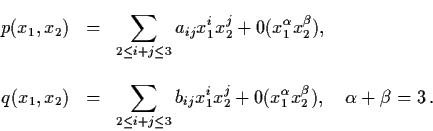
![]() ,
then a Hopf bifurcation occurs at the
origin of system (4.42) at the bifurcation value
,
then a Hopf bifurcation occurs at the
origin of system (4.42) at the bifurcation value ![]() ;
in particular, if
;
in particular, if
![]() ,
then system
(4.42) has a one-parameter family of stable limit cycles
for
,
then system
(4.42) has a one-parameter family of stable limit cycles
for ![]() and no limit cycles for
and no limit cycles for
![]() ,
and if
,
and if
![]() ,
then system (4.42) has
a one-parameter family of unstable limit cycles for
,
then system (4.42) has
a one-parameter family of unstable limit cycles for
![]() and no limit cycles for
and no limit cycles for
![]() .
.