Next: Hopf bifurcations Up: Periodic Solutions and Bifurcations Previous: Lienard systems

4.5 Structural stability and bifurcation

When we model a physical system by means of differential equations, it is not generally possible to take into account all the causes which determine the evolution. In other words, we have to admit that there are small perturbations acting on the vector fields of the differential system which can not be accurately estimated, consequently the validity of the description of the evolution as given by the flow of the differential system needs to be examined. In this section, we address the question of how the qualitative behaviour of the system

x' = f(x)

(4.27)

changes as we change the function or vector field f(x). If the qualitative behaviour remains the same for all ``nearby'' vector fields $\tilde{f} (x)$ , then system (4.27) is said to be structurally stable. The difference between Lyapunov stability discussed earlier and structural stability is that the former is concerned with perturbation of initial conditions or a periodic orbit and the latter is concerned with perturbation of the vector field.

To make the concept of structural stability precise, we need to define a norm of f.

Let $f \in C^{1} (\Omega )$ , $\Omega \subset R^{n}$ is an open set, then the C¹-norm of f on $\Omega$ is defined by

$\begin{displaymath}\parallel f \parallel_{1} = \sup_{x \in \Omega} \mid f(x) \mid + \sup_{x \in \Omega} \parallel D f(x) \parallel \, . \end{displaymath}$

(4.28)

Clearly, if K is a compact subset of $\Omega$ , then the C¹-norm of f on K is

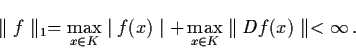
$\begin{displaymath}\parallel f \parallel_{1} = \max_{x \in K} \mid f(x) \mid + \max_{x \in K} \parallel Df(x) \parallel < \infty \, . \end{displaymath}$

Definition 4.5.1: Let $f \in C^{1} (\Omega )$ . Then system (4.27) is said to be structurally stable if there exists an $\veps > 0$ such that for all $\tilde{f} \in C^{1}(\Omega )$ with

$\begin{displaymath}\parallel f - \tilde{f} \parallel_{1} < \veps \, , \end{displaymath}$

system (4.27) is topologically equivalent to the system

$\begin{displaymath}x' = \tilde{f} (x) \, , \end{displaymath}$

(4.29)

i.e. there exists an orientation preserving homeomorphism $h : \Omega \raro \Omega$ which maps trajectories of (4.27) onto trajectories of (4.29).

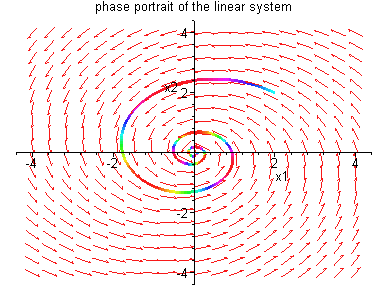
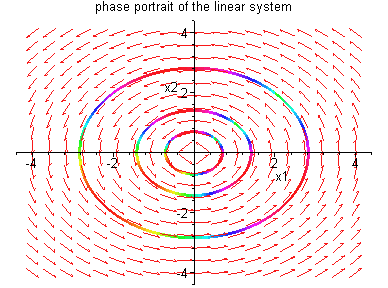
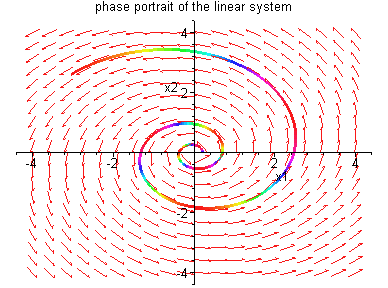
Example 4.5.1: Consider the linear system

$\begin{displaymath}\left\{ \begin{array}{l} x_{1}' = - x_{2} \, , \\ x_{2}' = x_{1} \, . \end{array} \right. \end{displaymath}$

(4.30)

We are going to show that the system (4.30) is not structurally stable. Let
$\Omega = \{ x \in R^{2}$ , $\mid x \mid < \rho , \, \rho > 0 \}$ , and consider the perturbed system

$\begin{displaymath}\left\{ \begin{array}{l} x_{1}' = - x_{2} + \mu x_{1}, \\ x_{2}' = x_{1} + \mu x_{2} \, . \end{array} \right. \end{displaymath}$

(4.31)

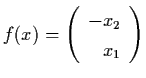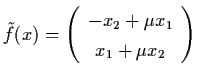Then $f(x) = \left( \begin{array}{r} - x_{2} \\ x_{1} \end{array} \right)$ , $\tilde{f} (x) = \left( \begin{array}{c} - x_{2} + \mu x_{1} \\ x_{1} + \mu x_{2} \end{array}\right)$ and $\parallel f - \tilde{f} \parallel_{1} = \mid \mu \mid (\mid x \mid + 1)$ . Thus for any $\veps > 0$ , we choose $\mid \mu \mid = \frac{\veps}{\rho + 2}$ . Then $\parallel f - \tilde{f} \parallel_{1} < \veps$ . But from the phase portraits for system (4.31) given below,

we see that system (4.30) and system (4.29) are not topologically equivalent. Thus system (4.30) is not structurally stable. In fact, it can be proved by contradiction. Suppose that system (4.30) and system (4.31) are topologically equivalent. Let $\phi_{t}$ and $\psi_{t}$ be the flows defined by (4.30) and (4.31) respectively. Then there is a homeomorphism $h : \Omega \raro \Omega$ and a strictly increasing, continuous function $t(\tau )$ mapping R onto R such that

$\begin{displaymath}h \circ \phi_{t(\tau )} (x_{0}) = \psi_{\tau } \circ h (x_{0}), \quad \forall \; x_{0} \in \Omega \, . \end{displaymath}$

(4.32)

Choose $x_{0} \in \Omega$ and $x_{0} \neq 0$ . Then ${\dss\lim_{t \raro \infty}} \phi_{t} (x_{0}) \neq 0$ . But for $\mu < 0$ , ${\dss\lim_{\tau \raro \infty}} \psi_{\tau} (x_{0}) = 0$ for any $x \in \Omega$ . Thus from (4.30)

$\begin{displaymath}\lim_{t \raro \infty} \phi_{t} (x_{0}) = \lim_{\tau \raro \in... ...aro \infty} \psi_{\tau} (h(x_{0}) \right) = h^{-1} (0) = 0\, , \end{displaymath}$

which is a contradiction. Thus system (4.30) and system (4.31) are not topologically equivalent.

As in Example 4.5.1, differential equations that model physical systems often contain parameters which may not be known with great accuracy. Thus one wants to know whether changes in the values of the parameters will cause qualitative changes in the asymptotic behaviour of the physical system. In system (4.31) of Example 4.5.1, the parameter $\mu$ changes from $\mu = 0$ to $\mu \neq 0$ and results in qualitative changes in the long term behaviour of solutions. The number $\mu = 0$ is called a bifurcation value for system (4.31). A formal definition is given below

Consider the system

$\begin{displaymath}x' = f (x, \mu ) \, , \end{displaymath}$

(4.33)

where $\mu \in R^{k}$ is a parameter.

Definition 4.5.2: A value $\mu_{0}$ of system (4.33) for which it is not structurally stable is called a bifurcation value of $\mu$ .

The simplest bifurcations are those for which the lack of structural stability is due to the presence of a non-hyperbolic equilibrium point. Here are some examples.

Example 4.5.2: Consider the one-dimensional system

$\begin{displaymath}x' = \mu - x^{2} \, . \end{displaymath}$

(4.34)

For $\mu > 0$ there are two equilibrium points $x = \pm \sqrt{\mu}$ ; $Df(x, \mu )= - 2x$ . $Df(\pm \sqrt{\mu}, \mu ) = \mp 2 \sqrt{\mu}$ . Thus $x = \sqrt{\mu}$ is asymptotically stable and $x = - \sqrt{\mu}$ is unstable.

For $\mu = 0$ , there is only one equilibrium point x = 0, Df(0,0) = 0. For $\mu < 0$ , there is no equilibrium point.

Thus $\mu = 0$ is a bifurcation value since the differential equation x' = -x² is not structurally stable. The phase portraits and the bifurcation diagram are given below.

Figure 4.5.1: The phase portraits for system (4.5.8)

Figure 4.5.2: The bifurcation diagram

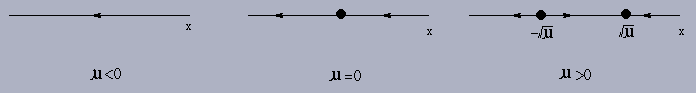
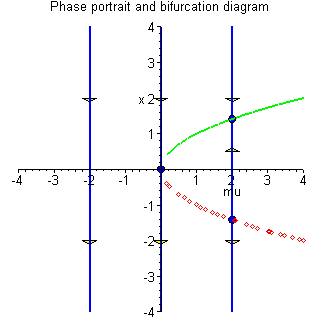
This type of bifurcation is called a saddle-node bifurcation.

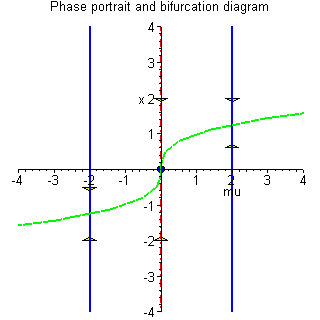
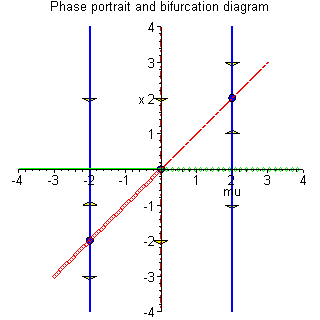
Example 4.5.3: Consider the one-dimensional system

$\begin{displaymath}x' = \mu x - x^{2} \, . \end{displaymath}$

(4.35)

For $\mu \neq 0$ , there are two equilibrium points x = 0, $\mu$ . For $\mu = 0$ , there is only one equilibrium point x = 0. $Df (x, \mu ) = \mu - 2x$ .

$\begin{displaymath}Df (0, \mu ) = \mu , \quad Df (\mu , \mu ) = - \mu , \quad Df(0,0) = 0 \, . \end{displaymath}$

$\mu = 0$ is a bifurcation value. The phase portraits and the bifurcation diagram are given below.

Figure 4.5.3: Phase portraits for (4.5.9)

This type of bifurcation is called transcritical bifurcation.

Figure 4.5.4: Bifurcation diagram

Example 4.5.4: Consider the one-dimensional system

$\begin{displaymath}x' = \mu x - x^{3} \, . \end{displaymath}$

(4.36)

For $\mu > 0$ , there are three equilibrium points, x = 0, $\pm \sqrt{\mu}$ . $Df(x, \mu ) = \mu - 3x^{2}$ , $Df(0, \mu ) = \mu$ , $Df \left( \pm \sqrt{\mu}, \mu \right) = - 2\mu$ . Thus x=0 is unstable and $x = \pm \sqrt{\mu}$ are asymptotically stable.

For $\mu = 0$ , there is only one equilibrium point x = 0 which is non-hyperbolic since Df (0,0) = 0.

For $\mu < 0$ , there is only one equilibrium point x = 0. $Df(0, \mu ) = \mu$ . Thus x = 0 is asymptotically stable. Thus $\mu = 0$ is a bifurcation value. The phase portraits and bifurcation diagram are shown below.

Figure 4.5.5: Phase portraits for (4.5.10)

This type of bifurcation is called a pitchfork bifurcation.

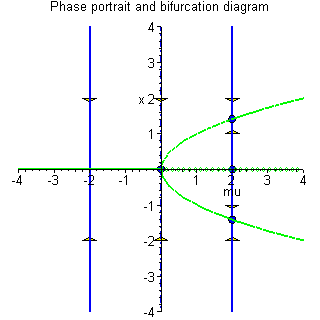
Figure 4.5.6: Bifurcation diagram for (4.5.10)

It should be noted that an equilibrium point is non-hyperbolic is a necessary but not sufficient condition for bifurcation to occur.

Example 4.5.5: Consider the one-dimensional system

$\begin{displaymath}x' = \mu - x^{3}. \end{displaymath}$

(4.37)

For any $\mu \in R$ , there is only one equilibrium point, $x = ^{~~3}\!\!\!\sqrt{\mu}$ . $Df \left(\!\!\!^{~~3}\!\!\!\sqrt{\mu}, \mu \right) = - 3 (\!\!\!^{~~3}\!\!\!\sqrt{\mu})^{2}$ . Df (0,0) = 0. Thus when $\mu = 0$ the equilibrium point x = 0 is non-hyperbolic. But $x = ^{~~3}\!\!\!\!\sqrt{\mu}$ is asymptotically stable. Thus $\mu = 0$ is not a bifurcation value.

Figure 4.5.7: Phase portraits in the $(x, \mu)$ -plane

Next: Hopf bifurcations Up: Periodic Solutions and Bifurcations Previous: Lienard systems