


Next: Definitions and notations
Up: Introduction
Previous: Introduction
Let us consider the systems of ordinary
differential equations (ODEs) having the form
where
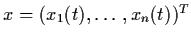 and
and
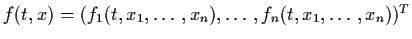 .
In general, there are
no known methods of solving system (1.1), even when
f(t,x) is linear, i.e.
f(t,x) = A(t) x + b(t),
and (1.1) reduces to a linear system of the form
.
In general, there are
no known methods of solving system (1.1), even when
f(t,x) is linear, i.e.
f(t,x) = A(t) x + b(t),
and (1.1) reduces to a linear system of the form
where
A(t) = (aij(t)), 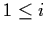 ,
,
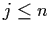 ,
is an
,
is an
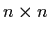 matrix whose entries are
functions of t and
matrix whose entries are
functions of t and
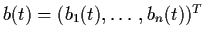 .
This, of course, is very disappointing.
However, it is not necessary, in most applications to find
the solutions of (1.1) explicitly. For example, let
x1(t) and x2(t) denote the populations,
at time t, of two species competing amongst
themselves for the limited food and living space in their
microcosm. Suppose, moreover, that the rates of growth of
x1(t) and x2(t) are governed by system
(1.1) with n=2. In this case, we are not really
interested in the values of x1(t) and
x2(t) at every time t. Rather,
we are interested in the qualitative properties of
x1(t) and x2(t). Specifically, we wish to
answer the following questions: Do there exist values
.
This, of course, is very disappointing.
However, it is not necessary, in most applications to find
the solutions of (1.1) explicitly. For example, let
x1(t) and x2(t) denote the populations,
at time t, of two species competing amongst
themselves for the limited food and living space in their
microcosm. Suppose, moreover, that the rates of growth of
x1(t) and x2(t) are governed by system
(1.1) with n=2. In this case, we are not really
interested in the values of x1(t) and
x2(t) at every time t. Rather,
we are interested in the qualitative properties of
x1(t) and x2(t). Specifically, we wish to
answer the following questions: Do there exist values
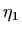 and
and 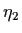 for the populations of
each species at which both species co-exist together in a
steady state? In other words are there numbers
for the populations of
each species at which both species co-exist together in a
steady state? In other words are there numbers
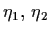 such that
such that
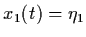 ,
,
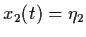 is a solution of
(1.1)? Such values
is a solution of
(1.1)? Such values
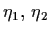 ,
if
they exist, are called equilibrium values of (1.1).
Suppose that the two species are co-existing in equilibrium
and we suddenly add a few members of species 1 to the
microcosm. Will x1(t) and x2(t) remain
close to their equilibrium values for all future times? Or
perhaps the extra few members give species 1 an added
advantage and cause the extinction of species 2.
Suppose that x1(t) and x2(t) have arbitrary values at t=0. What happens as t approaches infinity? Will one species ultimately emerge
victorious or will the struggle for existence end in a
draw? Other examples of a similar nature can be found in
physical sciences, engineering, etc. More generally, we
are interested in determining the following properties of
solutions of (1.1):
,
if
they exist, are called equilibrium values of (1.1).
Suppose that the two species are co-existing in equilibrium
and we suddenly add a few members of species 1 to the
microcosm. Will x1(t) and x2(t) remain
close to their equilibrium values for all future times? Or
perhaps the extra few members give species 1 an added
advantage and cause the extinction of species 2.
Suppose that x1(t) and x2(t) have arbitrary values at t=0. What happens as t approaches infinity? Will one species ultimately emerge
victorious or will the struggle for existence end in a
draw? Other examples of a similar nature can be found in
physical sciences, engineering, etc. More generally, we
are interested in determining the following properties of
solutions of (1.1):
- 1.
- Do there exist equilibrium values for which
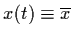 is a solution of (1.1)?
is a solution of (1.1)?
- 2.
- Let
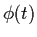 be a solution of (1.1). Suppose
that
be a solution of (1.1). Suppose
that 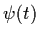 is a second solution with
is a second solution with
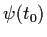 very close to
very close to
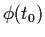 ;
i.e.
;
i.e.
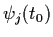 is very close to
is very close to
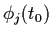 ,
,
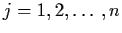 .
Will
.
Will 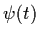 remain close to
remain close to 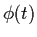 as t approaches
infinity? This question is often referred to as the
problem of stability. It is the most fundamental problem
in the qualitative theory of differential equations and has
occupied the attention of many mathematicians for the past
hundred years.
as t approaches
infinity? This question is often referred to as the
problem of stability. It is the most fundamental problem
in the qualitative theory of differential equations and has
occupied the attention of many mathematicians for the past
hundred years.
- 3.
- What happens to solution x(t) of (1.1) as
t approaches infinity? Do all solutions approach
equilibrium values? If they don't approach equilibrium
values, do they at least approach a periodic solution?



Next: Definitions and notations
Up: Introduction
Previous: Introduction