


Next: Equilibrium points and linearization
Up: Introduction
Previous: Qualitative analysis
For any
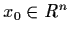 and
and
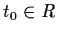 ,
the system
,
the system
together with the initial condition
is defined to be an initial value problem (IVP).
A function y(t) is said to be a solution of
the IVP (1.3)-(1.4) if
y' (t) = f(t,y(t)) and
y(t0) = x0. Of course, for an IVP, we are
concerned with the problem of existence of a unique
solution. This is guaranteed if the function f(t,x) is ``well-behaved'' or ``smooth enough''. You may have
seen the requirements on f in the scalar case and
we shall return to this point later.
If all the
fi (t,x) in (1.3) are independent
of t, then the system (1.3) is said to be autonomous and in this case it is often written as
Generally, system (1.5) is easier to deal with than that
of (1.3). Of course, strictly speaking, all the systems
should be nonautonomous since in the real world nothing
is permanent except change. But in many situations,
autonomous systems do give very good approximations and
therefore we are often content with them. In this course,
we shall devote our attention mainly on system (1.5)
while the general system (1.3) will be treated in more
advanced courses (e.g. AM 751). For autonomous system
(1.5), the value of t0 in the initial condition
(1.4) is insignificant and usually set to be 0.
Higher order equations of the form
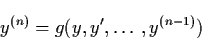 |
(1.6) |
can be reduced to a 1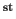 -order system of the form
-order system of the form
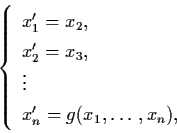 |
(1.7) |
by defining new variables
Example 1.2.1: Mass-spring system
Let y1 be the displacement of mass m1
from its equilibrium position, and
let y2 be the displacement of mass m2
from its equilibrium position.
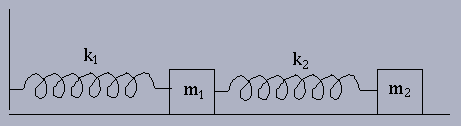
Assume Hooke's law for forces exerted by springs and
assume there is no friction. Application of Newton's law
gives
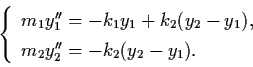 |
(1.8) |
Letting
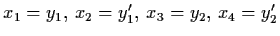 ,
then (1.8) reduces to
,
then (1.8) reduces to
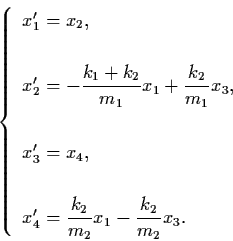 |
(1.9) |
For a vector
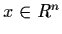 ,
we define the Euclidean
``norm''
,
we define the Euclidean
``norm''
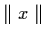 by
by
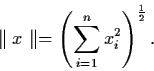 |
(1.10) |
The distance between any two points
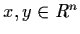 is defined by
is defined by
![\begin{displaymath}\parallel x - y \parallel = \left[ \sum_{i=1}^{n} (x_{i} -
y_{i})^{2} \right]^{\frac{1}{2}} = d (x,y).
\end{displaymath}](img35.gif) |
(1.11) |
It is evident that (1.10) defines the distance between
x and 0. Of course, there are other norms which
could be used, e.g.
In general, we define a norm on Rn to be any
function
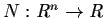 satisfying the following
conditions:
satisfying the following
conditions:
- 1.
-
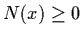 and N(x) = 0 iff x =0;
and N(x) = 0 iff x =0;
- 2.
-
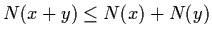 ;
;
- 3.
-
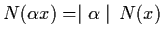
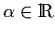 .
.
It should be noted that in finite dimensional spaces such
as Rn, all norms are equivalent. This is stated
in the following Lemma.
Lemma 1.2.1 Let
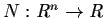 be
any norm. Then there exist constants A > 0, B >0
such that
be
any norm. Then there exist constants A > 0, B >0
such that
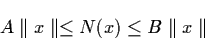 |
(1.12) |
for all x, where
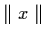 is
the Euclidean norm.
is
the Euclidean norm.
Proof: (Hirsch & Smale, P. 78-9)
We say x converges to y, denoted as 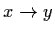 if
if
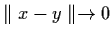 .
Clearly
.
Clearly 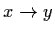 iff
iff
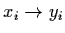 ,
,
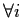 .
.



Next: Equilibrium points and linearization
Up: Introduction
Previous: Qualitative analysis
![]() and
and
![]() ,
the system
,
the system

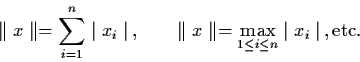
![]() satisfying the following
conditions:
satisfying the following
conditions:
![]() be
any norm. Then there exist constants A > 0, B >0
such that
be
any norm. Then there exist constants A > 0, B >0
such that
![]() if
if
![]() .
Clearly
.
Clearly ![]() iff
iff
![]() ,
,
![]() .
.