1.3 Equilibrium points and linearization

A point $\ol{x} \in R^{n}$ is said to be an equilibrium point of the system

 

x' = f(x) (1.13)

if $f(\ol{x}) = 0$. Clearly $\ol{x}$ is an equilibrium point of (1.13) iff $x(t) = \ol{x}$ is a constant solution of (1.13).

Example 1.3.1:     Consider the Lotka-Volterra model for a predator-prey population

$$\left\{ \begin{array}{l} x_{1}' = a x_{1} - b x_{1} x_{2}, \\... ...+ d x_{1} x_{2} \, , \quad a, b, c, d > 0, \end{array} \right.$$ (1.14)

where x₁ and x₂ represent the population of prey and predator at time t respectively. There are two equilibrium points: (0,0), $\left( \frac{c}{d} \, , \,\, \frac{a}{b} \right)$.

Example 1.3.2:     The simple pendulum equation

$$\left\{ \begin{array}{l} x_{1}' = x_{2}, \\ x_{2}' = - \alpha x_{2} - \sin x_{1}, \quad \alpha > 0 ,\end{array} \right.$$ (1.15)

has equilibrium points: $(n \pi , 0)$, $n \in \Zeal$.

As mentioned in §1.1, we are interested in the stability of equilibrium states. In order to address this question it is necessary to study the behaviour of the orbits of the ODEs close to the equilibrium points.

The idea is to consider the linear approximation of f at an equilibrium point. We thus assume that f has continuous partial derivatives with respect to x. The derivatives of f is an $n \times n$ matrix Df defined by

$$Df = \left( \frac{\partial f_{i}}{\partial x_{j}} \right) \, , \quad i,j=1,2, \ldots , n .$$ (1.16)

Let x be close to the equilibrium point $\ol{x}$. Then by Taylor's theorem we have

$$\begin{eqnarray*}f(x) & = & f(\ol{x}) + Df (\ol{x}) \cdot (x - \ol{x}) + R(\ol{x}, x) \\ & = & Df (\ol{x}) \cdot (x - \ol{x}) + R(\ol{x}, x), \end{eqnarray*}$$

where $R(\ol{x}, x)/\parallel x - \ol{x} \parallel \raro 0$ as $x\raro\ol{x}$.

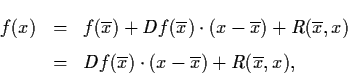
Thus the non-linear system (1.13) can be written as

$$x' = Df (\ol{x}) \cdot (x - \ol{x}) + R(\ol{x}, x) \, .$$ (1.17)

The linear system

$$y' = Df (\ol{x}) y \, ,\quad \mbox{where} \quad y = x - \ol{x}$$ (1.18)

is called the linearization of the nonlinear system (1.13).

Remark:     Any nonzero equilibrium point can be transformed into a zero equilibrium point by making the change of variable $z = x - \ol{x}$. Thus we often assume that $\ol{x} = 0$ is an equilibrium point of (1.13).

Question:     Do the solutions of (1.18) approximate those of (1.13) near $x = \ol{x}$?

This question will be answered later. For the moment, we state that in general the approximation is valid but that in special situations the approximation can fail.

In any event, this question suggests that a systematic study of linear ODEs is necessary before we can embark on the qualitative analysis of nonlinear ODEs.

Exercise 1.3.1:     Compute the linearization of systems (1.14) and (1.15) at their equilibrium points.