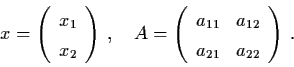
Consider the linear system
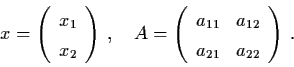
![\begin{displaymath}\left[ \begin{array}{cc}
\lambda_{1} & 0 \\
0 & \lambda_{2} ...
...\
- \beta & \alpha \end{array} \right] \, , \, \beta > 0 \, ,
\end{displaymath}](img66.gif)
Let's begin by describing the phase portraits of system (2.2).
Case I:
![$B = \left[ \begin{array}{cc}
\lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array} \right]$](img67.gif)
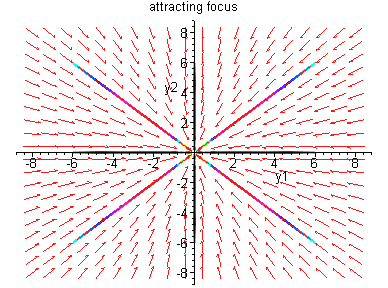
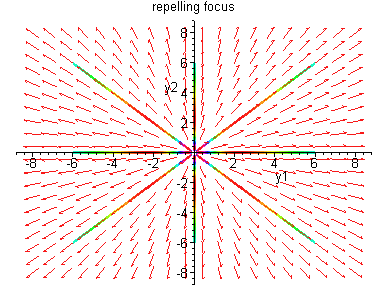
All solutions are half lines which approach (leave) (0,0).
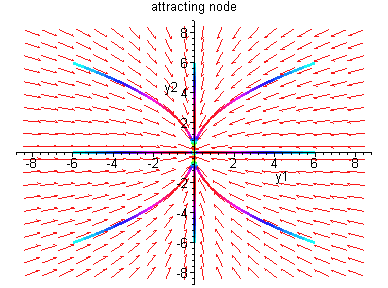
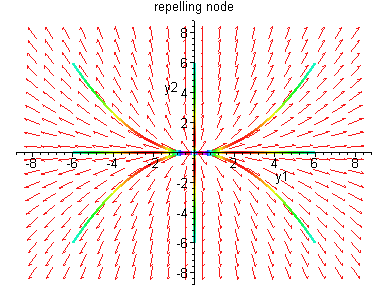
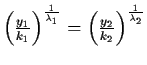
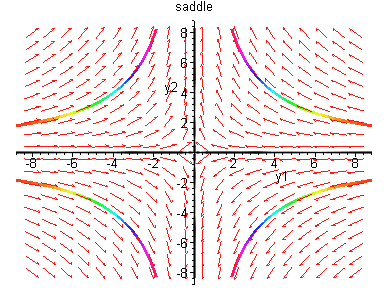
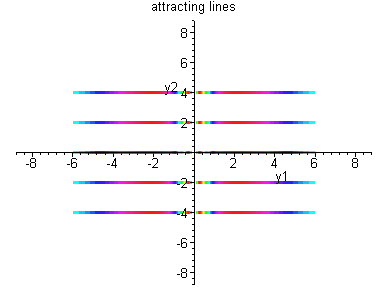
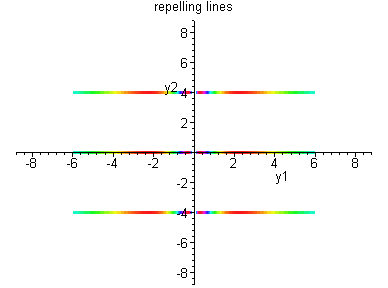
Case II:
![$B = \left[ \begin{array}{cc}
\lambda & 1 \\ 0 & \lambda \end{array} \right]$](img70.gif)
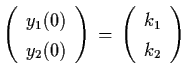 .
.
If
![]() and
and
![]() ,
then
,
then
![$y_{1} = y_{2} \left[ \frac{k_{1}}{k_{2}} +
\frac{1}{\lambda} \ln \left( \frac{y_{2}}{k_{2}} \right)
\right]$](img75.gif) .
.
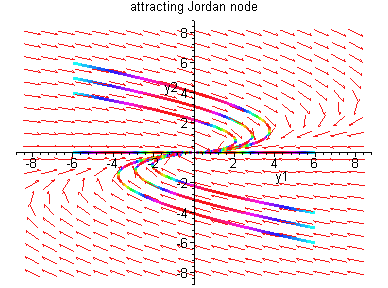
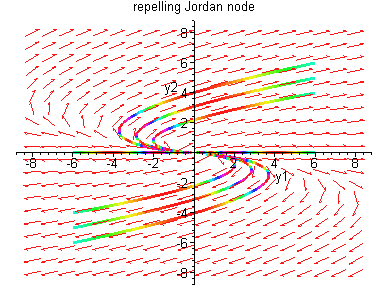
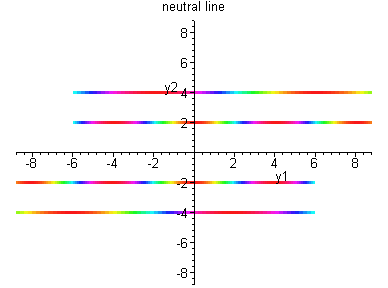
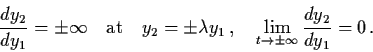
Case III:
![$B = \left[ \begin{array}{rc}
\alpha & \beta \\ - \beta & \alpha \end{array} \right] \,
, \quad \beta > 0$](img78.gif) .
.
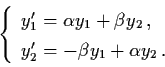
Thus the solution is
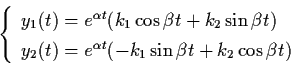
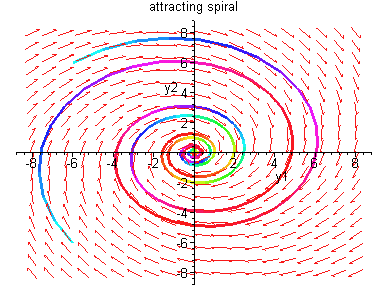
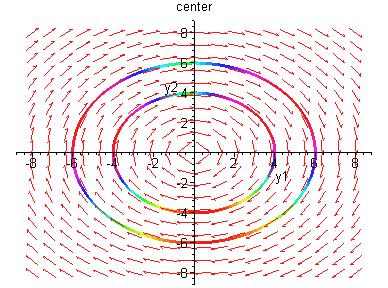
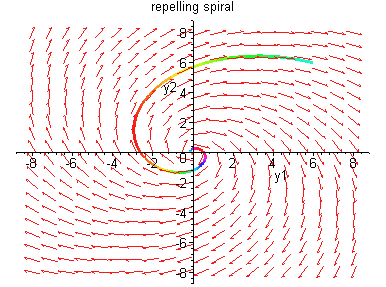
Remark: All the phase portraits we have made so
far are in terms of the canonical coordinates y.
You may wonder what the portraits look like in terms of
the original coordinates x. Here are some examples
Example 2.1.1: Consider the system x' = Ax,
where
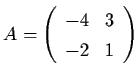 .
.

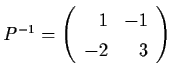 .
Then y' =
By, where
.
Then y' =
By, where
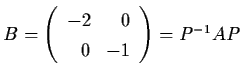 .
.

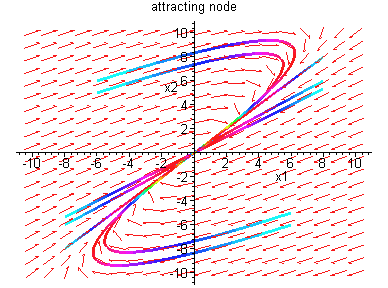
Example 2.1.2: Consider the system x' = Ax,
where
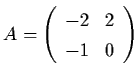 .
Let
.
Let
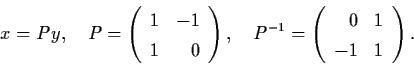
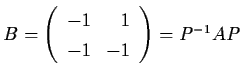 .
.
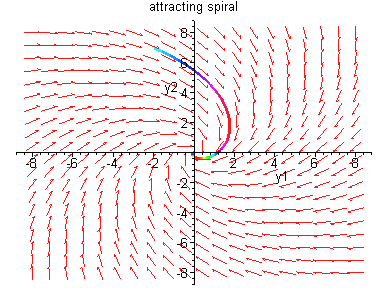
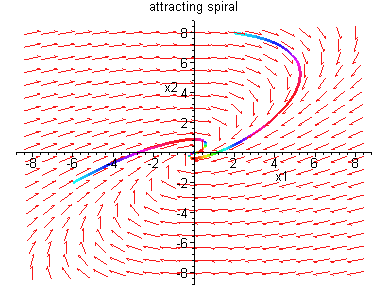
Remark: It should be noted that systems x' =
Ax and
x' = kAx, k > 0, have identical phase portraits.