


Next: Distinct eigenvalues
Up: Linear Systems
Previous: Linear systems in R
The IVP in one-dimensional space
has a unique solution
x(t) = x0 eat, 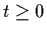 .
It is natural to ask whether we can define the
``exponential of a matrix'' so that the IVP in
.
It is natural to ask whether we can define the
``exponential of a matrix'' so that the IVP in
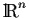
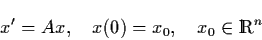 |
(2.3) |
has a unique solution
x(t) = eAt x0, 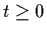 .
Before answering this question, we need to define
the norm of a linear operator and the exponential of
matrices. Let
.
Before answering this question, we need to define
the norm of a linear operator and the exponential of
matrices. Let
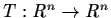 be a linear operator. We define the norm of T by
be a linear operator. We define the norm of T by
where
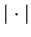 denotes the Euclidean norm.
Let the linear operator T on Rn be
represented by the
denotes the Euclidean norm.
Let the linear operator T on Rn be
represented by the
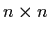 matrix A
with respect to a basis for Rn. Then the norm of
A is defined by
matrix A
with respect to a basis for Rn. Then the norm of
A is defined by
Let L(Rn) be the space of all linear operators
on Rn. Then for
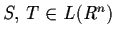 ,
,
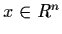 ,
,
- (1)
-
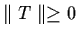 and
and
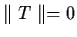 iff T=0;
iff T=0;
- (2)
-
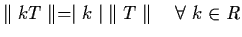 ;
;
- (3)
-
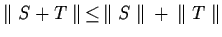 ;
;
- (4)
-
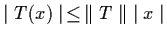
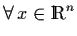 ;
;
- (5)
-
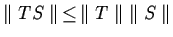 ;
;
- (6)
-
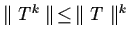
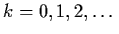 .
.
Proof: (omitted)
Lemma 2.2.1: Let A be an
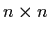 matrix and
matrix and
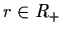 .
Then the series
.
Then the series
is absolutely and uniformly convergent for
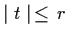 .
.
Proof: (omitted)
Definition 2.2.1: Let A be an
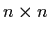 matrix. Then
matrix. Then
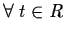 ,
we
define
,
we
define
Let 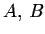 and P be
and P be
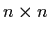 matrices where P is nonsingular. Then
matrices where P is nonsingular. Then
- (1)
- e0 = I, 0 being
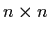 zero
matrix;
zero
matrix;
- (2)
-
eA+B = eA eB, provided AB = BA;
- (3)
- eA is invertible and
(eA)-1 = e-A;
- (4)
-
P-1 AP = B implies
eB = P-1 eA P.
Remark: eAt is an
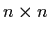 matrix whose entries are limits of the corresponding
n2 infinite series.
matrix whose entries are limits of the corresponding
n2 infinite series.
Theorem 2.2.1: Let A be an
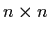 matrix. Then IVP (2.3) has a unique solution for
all
matrix. Then IVP (2.3) has a unique solution for
all 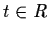 which is given by
which is given by
Proof: (Omitted)
Corollary 2.2.1 By Theorem 2.2.1, we have
- (1)
-
![$e^{\tiny\left[ \begin{array}{ll}
\lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array}...
...{array}{ll}
e^{\lambda_{1}t} & 0 \\ 0 & e^{\lambda_{2}t} \end{array}\right]\, ;$](img129.gif)
- (2)
-
![$e^{\tiny\left[ \begin{array}{ll}
\lambda & 1 \\ 0 & \lambda \end{array} \right]t} =
e^{\lambda t} \left[ \begin{array}{ll}
1 & t \\ 0 & 1 \end{array} \right]\, ;$](img130.gif)
- (3)
-
![$e^{\tiny\left[ \begin{array}{rl}
\alpha & \beta \\ - \beta & \alpha \end{array}...
...cos \beta t & \sin \beta t \\ - \sin \beta t & \cos \beta
t \end{array} \right]$](img131.gif) .
.
Corollary 2.2.2 Let P be an
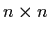 nonsingular matrix. If
P-1 AP = B,
then
x(t) = PeBt P-1 x0 is a solution
of the IVP (2.3).
nonsingular matrix. If
P-1 AP = B,
then
x(t) = PeBt P-1 x0 is a solution
of the IVP (2.3).
Exercise Perko, P. 19-20; 4, 6, 7, 8.



Next: Distinct eigenvalues
Up: Linear Systems
Previous: Linear systems in R
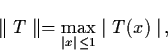
![]() matrix and
matrix and
![]() .
Then the series
.
Then the series
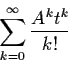
![]() matrix. Then
matrix. Then
![]() ,
we
define
,
we
define
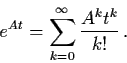
![]() and P be
and P be
![]() matrices where P is nonsingular. Then
matrices where P is nonsingular. Then
![]() matrix whose entries are limits of the corresponding
n2 infinite series.
matrix whose entries are limits of the corresponding
n2 infinite series.
![]() matrix. Then IVP (2.3) has a unique solution for
all
matrix. Then IVP (2.3) has a unique solution for
all ![]() which is given by
which is given by
![$e^{\tiny\left[ \begin{array}{ll}
\lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array}...
...{array}{ll}
e^{\lambda_{1}t} & 0 \\ 0 & e^{\lambda_{2}t} \end{array}\right]\, ;$](img129.gif)
![$e^{\tiny\left[ \begin{array}{ll}
\lambda & 1 \\ 0 & \lambda \end{array} \right]t} =
e^{\lambda t} \left[ \begin{array}{ll}
1 & t \\ 0 & 1 \end{array} \right]\, ;$](img130.gif)
![$e^{\tiny\left[ \begin{array}{rl}
\alpha & \beta \\ - \beta & \alpha \end{array}...
...cos \beta t & \sin \beta t \\ - \sin \beta t & \cos \beta
t \end{array} \right]$](img131.gif) .
.
![]() nonsingular matrix. If
P-1 AP = B,
then
x(t) = PeBt P-1 x0 is a solution
of the IVP (2.3).
nonsingular matrix. If
P-1 AP = B,
then
x(t) = PeBt P-1 x0 is a solution
of the IVP (2.3).