3.3 The flow defined by ODEs

In Section 2.5, we defined the (linear) flow $e^{At} : R^{n} \raro R^{n}$, of the linear system

$$x' = Ax \, .$$

The mapping $\phi_{t} = e^{At}$ satisfies, for all $x \in R^{n}$,

1.

$\phi_{0} (x) = x$

2.

$\phi_{t+s} (x) = \phi_{t} (\phi_{s} (x)) \, , \quad \forall \quad s, t \in R$.

In this section, we define the (nonlinear) flow, $\phi_{t}$, of the nonlinear system

 

x' = f(x) (3.12)

and show that it satisfies these same basic properties.

Let $\Omega \subset R^{n}$ be an open set. Suppose for any $x_{0} \in \Omega$ system (3.12) admits a unique solution x(t, x₀) existing on a maximal interval J(x₀). Then for any $t \in J (x_{0})$ we define a mapping $\phi_{t} : \Omega \raro \Omega$ by

$$\phi_{t} : x_{0} \raro x(t,x_{0}) \, .$$ (3.13)

The one-parameter family mappings $\phi_{t}$ is called the flow of the system (3.12). $\phi_{t}$ is called a local-flow if $J(x_{0}) = (\alpha^{*}, \beta^{*})$, $- \infty < \alpha^{*} < \beta^{*} < \infty$, a semi-flow if $- \infty < \alpha^{*} < \beta^{*} = \infty$ or $- \infty = \alpha^{*} < \beta^{*} < \infty$, and a global-flow if $- \infty = \alpha^{*}, \beta^{*} = \infty$, for all $x_{0} \in \Omega$.

Theorem 3.3.1:     Let $\phi_{t}$ be the flow associated with system (3.12). Suppose that for any $x_{0} \in \Omega$, system (3.12) admits a unique solution x(t, x₀) with x(0, x₀) = x₀. Then $\phi_{t}$ satisfies

(i)

$\phi_{0} (x_{0}) = x_{0}$

(ii)

$\phi_{t+s} (x_{0}) = \phi_{t} (\phi_{s} (x_{0}))$ provided $t, s \in J(x_{0})$ and $t + s \in J(x_{0})$.

Proof: (omitted)

Remark:     The flow $\phi_{t}$ describes all solutions of system (3.12) for all possible initial values x₀, and hence describes fully the evolution of the physical system. For a fixed t, $\phi_{t} : \Omega \raro \Omega$ gives the state of the system $\phi_{t}(x_{0})$ at time t for all initial states x₀. On the other hand, for a fixed $x_{0} \in \Omega$, $x(t, x_{0}) : J (x_{0}) \raro R^{n}$ gives the state of the system for all $t \in J (x_{0})$ with x(0) = x₀ initially.

If we only abstract, from the differential system (3.12), the one-parameter family of mappings $\phi_{t}$ which satisfies property (i) and (ii), then we call $\phi_{t}$ a dynamical system.

Definition 3.3.1:     A dynamical system is a C¹ map $\phi_{t} : R \times \Omega \raro R$ which satisfies

(i)

$\phi_{0} = I$;

(ii)

$\phi_{t+s} = \phi_{t} \circ \phi_{s}$, for $t, \, s \in R$.

Remark:     Let $\Omega$ be an open subset of Rⁿ. Then every dynamical system $\phi_{t}$ on $\Omega$ gives rise to a differential equation. In fact, define f by

$$f(x) = \frac{d}{dt} \phi_{t} (x) \Biggl\vert _{t=0} \, .$$

Then setting $x(t) = \phi_{t}(x)$, we have

$$\begin{eqnarray*}x' (t) = \frac{d}{dt} \phi_{t} (x) & = & \lim_{s \raro 0} \frac... ...phi_{t} (x)) \Biggl\vert _{s=0} = f(\phi_{t} (x)) = f(x(t)) \, , \end{eqnarray*}$$

i.e. x' (t) = f(x(t)).

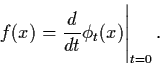
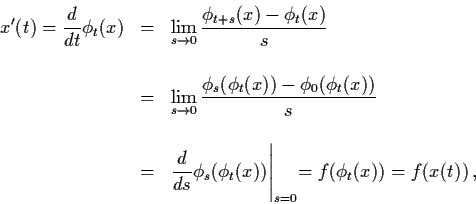
Conversely, given differential system (3.12), its flow $\phi_{t}$ defined by (3.13) may define a dynamical system. However, this converse process is much more complicated. We still need to investigate the dependence of the solutions of (3.12) on the initial value. To establish dependence of the solution on initial values we first give a result due to T.H. Gronwall, which is also of independent interest.

Lemma 3.3.1: (Gronwall)     Suppose that m(t) is a continuous real valued function that satisfies $m(t) \geq 0$ and

$$m(t) \leq c + k \int_{0}^{t} m(s)ds \, ,\quad c, k>0 \, ,\quad t \in [0, \alpha ] \, .$$

Then $m(t) \leq c e^{kt}$, $t \in [0, \alpha ]$.

Proof: (omitted)

Theorem 3.3.2:     Let $\Omega \in R^{n}$ be an open subset and f(x) satisfy a Lipschitz condition on $\Omega$, i.e. $\exists \; L > 0$

$$\mid f (x) - f(y) \mid \, \leq \, L \mid x-y \mid \, , \quad x, y \in\Omega \, .$$

Then the solution x(t, x₀) of (3.12) is continuous in x₀ for all $x_{0} \in \Omega$.

Proof: (omitted)

Theorem 3.3.3:     Let $f \in C^{1} (\Omega )$. Then the solution x(t, x₀) of (3.12) is continuously differentiable at x₀ for all $x_{0} \in \Omega$.

Proof:     See L. Perko, P. 79-82.

Thus, given differential system (3.12) with $f \in C^{1} (\Omega )$, $\Omega$ being an open subset of Rⁿ. Then the flow $\phi_{t}$ of (3.12) is a dynamical system if an only if $\forall \; x_{0} \in\Omega$, the solution of x(t, x₀) of (3.12) is defined for all $t \in R$, i.e. $J(x_{0}) = (- \infty , \infty )$. In this case, we say that $\phi_{t}$ is the dynamical system on $\Omega$ defined by (3.12). The following definition will be needed in the next section.

Definition 3.3.2:     Let $E \subset R^{n}$. Then E is called (i) a positively invariant set of (3.12) if $\phi_{t} E \subset E$ for all $t \geq 0$; (ii) a negatively invariant set of (3.12) if $\phi_{t} E \subset E$ for all $t \leq 0$; (iii) an invariant set if $\phi_{t} E \subset E$ for all $t \in R$.