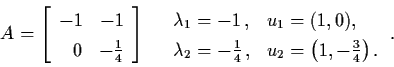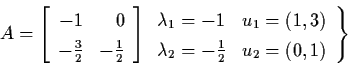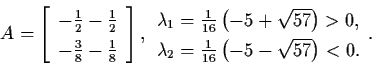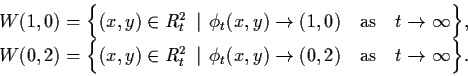


Next: Stability of equilibria
Up: Nonlinear Systems
Previous: The flow defined by
We showed in Section 3.1 that if 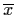 is a
nonlinear sink or source, then in a neighbourhood of
is a
nonlinear sink or source, then in a neighbourhood of
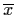 ,
the nonlinear system
,
the nonlinear system
has the same qualitative structure as the linear system
where
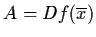 .
We shall show that this is true
if
.
We shall show that this is true
if 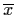 is a hyperbolic equilibrium point. The
general result is known as the Hartman-Grobman Theorem.
is a hyperbolic equilibrium point. The
general result is known as the Hartman-Grobman Theorem.
Let us begin with an example
Example 3.4.1: Consider the nonlinear system in
R2
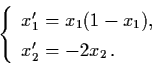 |
(3.16) |
This system has two equilibrium points (0,0) and
(1,0). The following are the linearizations of (3.16)
at these equilibria and their phase portraits.
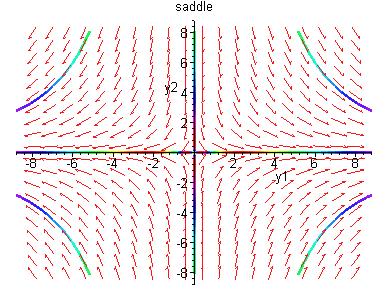
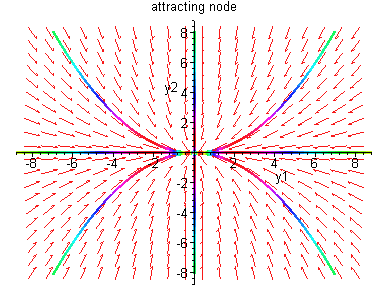
Linearization at (0,0).
Linearization at (1,0).
y' = Df (0,0) y,
y' = Df (1,0) y,
The solution of (3.16) can be solved explicitly as follows
The phase portrait is shown below.
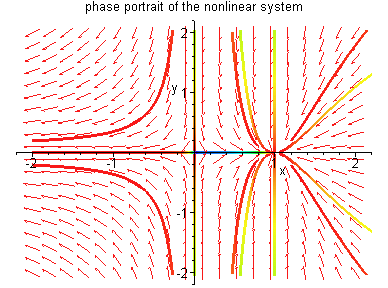
phase portrait of the nonlinear system
Example 3.4.1 Simulation
It is easy to see that the linearizations give a reliable
description of the nonlinear orbits near the equilibrium
points.
For convenience, we shall assume that the equilibrium point
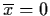 .
We need the following definition.
.
We need the following definition.
Definition 3.4.1: The systems (3.14) and
(3.15) are said to be topologically equivalent in a
neighbourhood of the origin if there exists a
homeomorphism
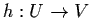 ,
where U and
V are some open sets containing the origin, which maps
trajectories of (3.14) in U onto those of (3.15)
in V and preserves the orientation. If, in
addition, h preserves the parameterization by time,
then (3.14) and (3.15) are said to be topologically
conjugate in a neighbourhood of the origin.
,
where U and
V are some open sets containing the origin, which maps
trajectories of (3.14) in U onto those of (3.15)
in V and preserves the orientation. If, in
addition, h preserves the parameterization by time,
then (3.14) and (3.15) are said to be topologically
conjugate in a neighbourhood of the origin.
Clearly, if two linear systems
x' = A1 x and
y' = A2 y in Rn are linearly equivalent,
then they are topologically equivalent. In fact, let k
> 0 and P be a nonsingular matrix such
that
Setting
y = h(x) = P-1 x, then
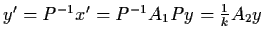 .
.
Let t = sk. Then
which implies
Thus the mapping h, which is clearly a
homeomorphism, maps trajectories of
x' = A1 x
onto trajectories of
y' = A2 y and preserves the
orientation since k > 0. In the case k=1,
h preserves the parameterization by time and thus the
two linear systems are topologically conjugate.
Theorem 3.4.1: (Hartman-Grobman) Let
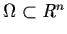 be an open set containing the origin, let
be an open set containing the origin, let
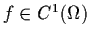 ,
and let
,
and let 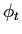 be
the flow of the nonlinear system (3.14). Suppose that
f(0) = 0 and the matrix A =Df(0) has no
eigenvalue with zero real part. Then there exists a
homeomorphism
be
the flow of the nonlinear system (3.14). Suppose that
f(0) = 0 and the matrix A =Df(0) has no
eigenvalue with zero real part. Then there exists a
homeomorphism
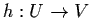 ,
U and V
being open sets containing the origin, such that
,
U and V
being open sets containing the origin, such that
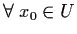
being an open interval containing zero.
Proof: See P. Hartman, Ordinary Differential
Equations, 2nd Ed., 1973, P. 244-250.
Theorem 3.4.1 tells us that h maps trajectories of
(3.14) in a neighbourhood of the equilibrium point onto
trajectories of (3.15) in a neighbourhood of the origin
and preserves the parameterization, and thus systems
(3.14) and (3.15) are topologically conjugate in a
neighbourhood of the origin.
Illustration:
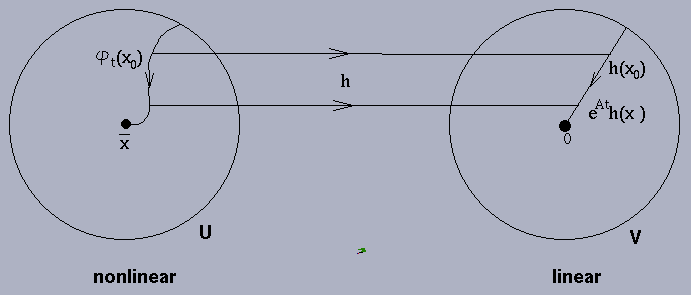
Remark: The above theorem was proved
independently by P. Hartman in 1960 and the Russian
mathematician D.M. Grobman in 1959.
Example 3.4.2: Consider the system
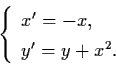 |
(3.17) |
The solution of (3.17) is given by
The linearization of (3.17) at (0,0) is
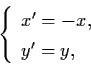 |
(3.18) |
whose solution is
Define the homeomorphism h by
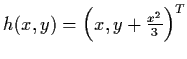 .
.
Then
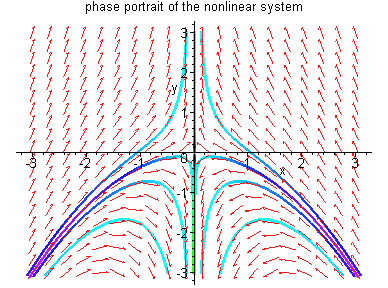
Example 3.4.2 Simulation
Remark:
- 1.
- In the above example, we actually have found a global
homeomorphism which maps trajectories of (3.17) onto
trajectories of (3.18). But this does not happen very
often in general.
- 2.
- The images of the stable and unstable subspaces of (3.18),
i.e. x-axis and y-axis, in Example 3.4.2, under the
mapping h-1 are the curves
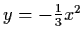 and y-axis, respectively, which are invariant
sets of (3.17). All solutions of (3.17) starting on the
curve
and y-axis, respectively, which are invariant
sets of (3.17). All solutions of (3.17) starting on the
curve
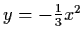 tend to the origin as
tend to the origin as
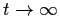 .
Moreover the curve
.
Moreover the curve
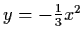 is tangent to the x-axis at the
origin.
is tangent to the x-axis at the
origin.
In general, if 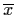 is a saddle point of the
system (3.14) with
is a saddle point of the
system (3.14) with
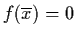 ,
then the images
of the stable subspace Es and the unstable
subspace of the linearized system (3.15), in a
neighbourhood of the origin, under the mapping h-1 are surfaces Ws and Wu, which are
called local stable manifold and local unstable
manifold of
,
then the images
of the stable subspace Es and the unstable
subspace of the linearized system (3.15), in a
neighbourhood of the origin, under the mapping h-1 are surfaces Ws and Wu, which are
called local stable manifold and local unstable
manifold of 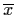 respectively, and can be
defined as follows:
respectively, and can be
defined as follows:
The relations between
Ws/Wu and
Es/Eu are given in the next theorem.
Theorem 3.4.2: (Stable/unstable manifold) Let
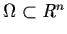 be an open set containing
be an open set containing
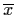 ,
let
,
let
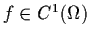 ,
and let
,
and let
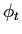 be the flow of the system (3.14). Suppose
that
be the flow of the system (3.14). Suppose
that
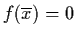 and that
and that
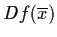 has
k eigenvalues with negative real parts and n-k eigenvalues with positive real parts. Then there exists
k-dimensional stable manifold Ws tangent to
Es at
has
k eigenvalues with negative real parts and n-k eigenvalues with positive real parts. Then there exists
k-dimensional stable manifold Ws tangent to
Es at 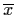 ,
and n-k-dimensional
unstable manifold Wu tangent to Eu at
,
and n-k-dimensional
unstable manifold Wu tangent to Eu at
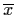 ,
such that Ws and Wu
are positively invariant and negatively invariant sets of
(3.14), respectively, and
,
such that Ws and Wu
are positively invariant and negatively invariant sets of
(3.14), respectively, and
Proof: See Perko, Differential
Equations/Dynamical Systems, P. 108-111.
Illustration:
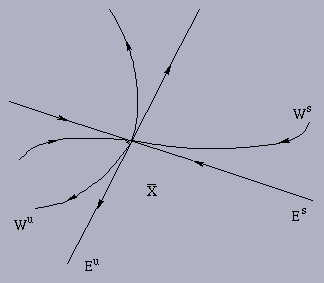 Remark: The stable and unstable manifolds
Ws and Wu, in Theorem 3.4.2, are only
defined in a small neighbourhood of the equilibrium point
Remark: The stable and unstable manifolds
Ws and Wu, in Theorem 3.4.2, are only
defined in a small neighbourhood of the equilibrium point
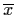 and are therefore referred to as local stable
and unstable manifolds. We define the global stable and
unstable manifolds of (3.14) at
and are therefore referred to as local stable
and unstable manifolds. We define the global stable and
unstable manifolds of (3.14) at 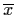 by letting
points in Ws flow backward in time and those in
Wu flow forward in time.
by letting
points in Ws flow backward in time and those in
Wu flow forward in time.
The global stable manifold of (3.14) at 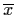 is
given by
is
given by
The global unstable manifold of (3.14) at 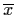 is given by
is given by
It can be shown that the global stable and unstable
manifolds
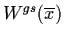 and
and
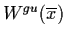 are unique, invariant and
are unique, invariant and
It is easy to see that the curve
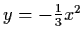 ,
in example 3.4.2, is the global stable manifold
and the y-axis is the global unstable manifold.
,
in example 3.4.2, is the global stable manifold
and the y-axis is the global unstable manifold.
The linearization of a non-linear system can fail to give
reliable information about the orbits, if a certain
restriction (hyperbolic) does not hold.
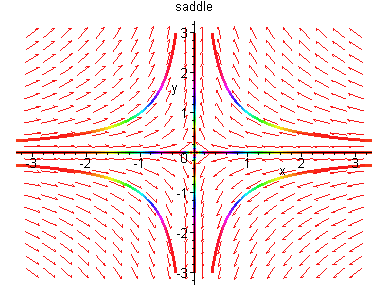
Example 3.4.3: Consider the nonlinear system
Then
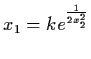 and the
origin is a nonlinear saddle.
and the
origin is a nonlinear saddle.
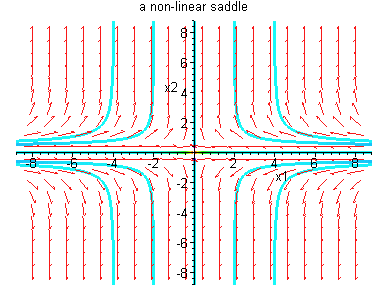 Linearization at (0,0) is given by
Linearization at (0,0) is given by
The phase portrait is shown on the right which illustrates
that linearization fails to give reliable information.
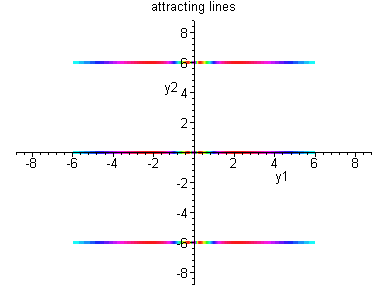
The source of the failure is that the matrix Df(0,0) has a zero eigenvalue.
Example 3.4.3 Simulation
Example 3.4.4: Consider the nonlinear system
which is a nonlinear spiral.
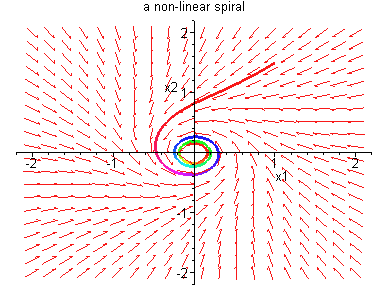
But the linearization at (0,0) is
which is a centre.
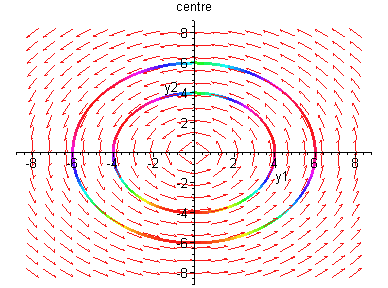
The source of the failure is that the matrix Df(0,0) has eigenvalues with zero real parts.
Finally, to conclude this section, we come back to the
population growth model which was considered in Section 3.2.
Example 3.4.4 Simulation
Example 3.4.5: Consider the nonlinear system
There are four equilibrium points.
- 1.
- (0,0), neither species win and there is natural
annihilation;
- 2.
- (1,0), ``A'' wins;
- 3.
- (0,2), ``B'' wins;
- 4.
-
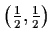 ,
a state of
coexistence.
,
a state of
coexistence.
By plotting the phase portrait, we would like to see the
initial conditions which, as
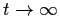 ,
would
give rise to the above equilibrium states.
,
would
give rise to the above equilibrium states.
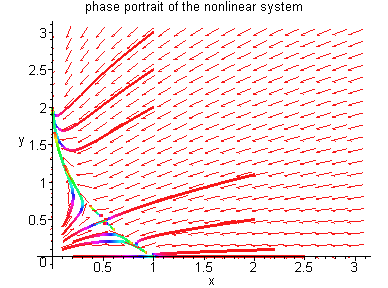
The first step is to characterize the nature of each
equilibrium point according to the linearization.
Case 1:
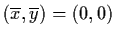 .
.
Thus (0,0) is a source.
Eigenvectors
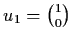 ,
,
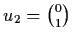 .
.
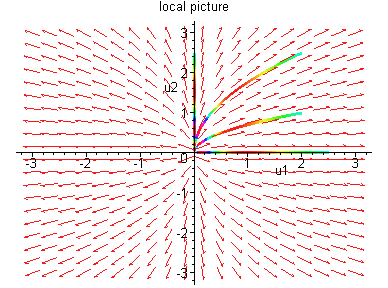 Case 2:
Case 2:
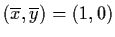 .
.
Thus (1,0) is a sink.
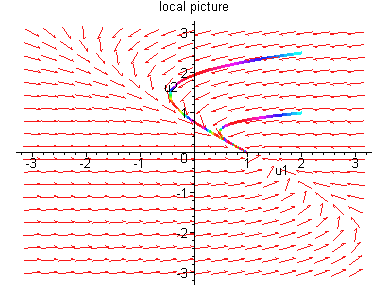 Case 3:
Case 3:
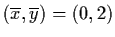 .
.
(0,2) is a sink.
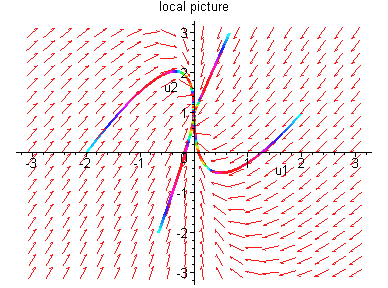 Case 4:
Case 4:
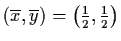 .
.
Thus
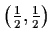 is a
saddle.
is a
saddle.
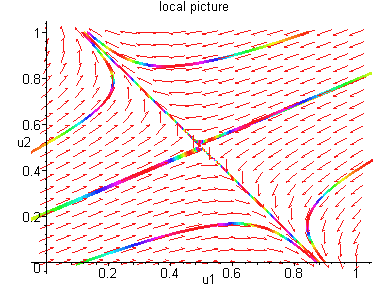 We may ``paste'' these local pictures onto a huge picture
of the phase plane as follows:
We may ``paste'' these local pictures onto a huge picture
of the phase plane as follows:
 Explanation:
Explanation:
- 1)
- Equilibrium points A and B, representing
``win'' of one species over another, are sinks, hence they
attract nearby solution trajectories. They are said to be
stable. (This will be formally defined and discussed in
the next section.)
- 2)
- The origin 0 is a source, being unstable - nearby
solution trajectories are repelled away, hence there is no
possibility that both populations would be eliminated.
- 3)
- The last equilibrium point represents peaceful coexistence,
and is a saddle and hence the chances of reaching it are
very rare. Only points which lie on the stable manifolds
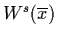 of the equilibrium points will be
attracted arbitrarily close to it. On the other hand,
virtually all other points
of the equilibrium points will be
attracted arbitrarily close to it. On the other hand,
virtually all other points
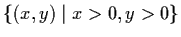 will be attracted to either (1,0) or (0,2).
will be attracted to either (1,0) or (0,2).
A more complete picture of the phase portrait is shown
below.
Example 3.4.5 Simulation
Remark: In applications, coexistence is very
important. To have coexistence, one should control the
population so that neither species will die out.
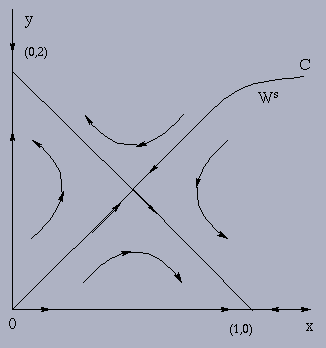 The curve C in the diagram, which is, in fact, the
stable manifold of the equilibrium point
The curve C in the diagram, which is, in fact, the
stable manifold of the equilibrium point
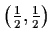 ,
separates regions of
the quadrant which are attracted to the equilibrium points
(1,0) and (0,2). These two regions are
formally called the basins of attraction of the
attractive equilibrium points (1,0) and (0,2) and are usually denoted by
,
separates regions of
the quadrant which are attracted to the equilibrium points
(1,0) and (0,2). These two regions are
formally called the basins of attraction of the
attractive equilibrium points (1,0) and (0,2) and are usually denoted by
The determination, or at least estimation, of the basins of
attraction of an equilibrium point, is an important aspect
of dynamical systems theory and its application. For
example, given a reasonable model of a mechanical system,
(e.g. bridge, electrical circuits, solar system), which has
a stable equilibrium  ,
to what points in
phase space can we perturb the system and be ensured that
the equations of motion of the system will bring it back to
that equilibrium point?
,
to what points in
phase space can we perturb the system and be ensured that
the equations of motion of the system will bring it back to
that equilibrium point?



Next: Stability of equilibria
Up: Nonlinear Systems
Previous: The flow defined by
![]() is a
nonlinear sink or source, then in a neighbourhood of
is a
nonlinear sink or source, then in a neighbourhood of
![]() ,
the nonlinear system
,
the nonlinear system


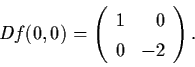
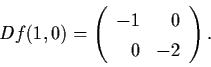
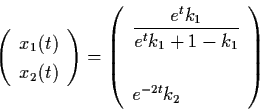

![]() .
We need the following definition.
.
We need the following definition.
![]() ,
where U and
V are some open sets containing the origin, which maps
trajectories of (3.14) in U onto those of (3.15)
in V and preserves the orientation. If, in
addition, h preserves the parameterization by time,
then (3.14) and (3.15) are said to be topologically
conjugate in a neighbourhood of the origin.
,
where U and
V are some open sets containing the origin, which maps
trajectories of (3.14) in U onto those of (3.15)
in V and preserves the orientation. If, in
addition, h preserves the parameterization by time,
then (3.14) and (3.15) are said to be topologically
conjugate in a neighbourhood of the origin.
![]() be an open set containing the origin, let
be an open set containing the origin, let
![]() ,
and let
,
and let ![]() be
the flow of the nonlinear system (3.14). Suppose that
f(0) = 0 and the matrix A =Df(0) has no
eigenvalue with zero real part. Then there exists a
homeomorphism
be
the flow of the nonlinear system (3.14). Suppose that
f(0) = 0 and the matrix A =Df(0) has no
eigenvalue with zero real part. Then there exists a
homeomorphism
![]() ,
U and V
being open sets containing the origin, such that
,
U and V
being open sets containing the origin, such that
![]()

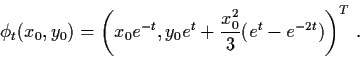
![\begin{displaymath}e^{At} \left( \begin{array}{l}
x_{0} \\ y_{0} \end{array} \ri...
...ft[ \begin{array}{rl}
-1 & 0 \\ 0 & 1 \end{array} \right] \, .
\end{displaymath}](img550.gif)
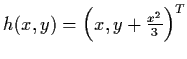 .
.
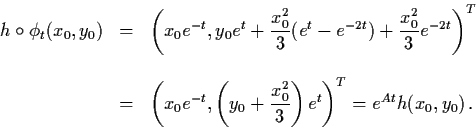


![]() is a saddle point of the
system (3.14) with
is a saddle point of the
system (3.14) with
![]() ,
then the images
of the stable subspace Es and the unstable
subspace of the linearized system (3.15), in a
neighbourhood of the origin, under the mapping h-1 are surfaces Ws and Wu, which are
called local stable manifold and local unstable
manifold of
,
then the images
of the stable subspace Es and the unstable
subspace of the linearized system (3.15), in a
neighbourhood of the origin, under the mapping h-1 are surfaces Ws and Wu, which are
called local stable manifold and local unstable
manifold of ![]() respectively, and can be
defined as follows:
respectively, and can be
defined as follows:
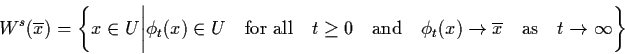
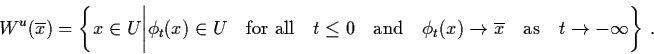
![]() be an open set containing
be an open set containing
![]() ,
let
,
let
![]() ,
and let
,
and let
![]() be the flow of the system (3.14). Suppose
that
be the flow of the system (3.14). Suppose
that
![]() and that
and that
![]() has
k eigenvalues with negative real parts and n-k eigenvalues with positive real parts. Then there exists
k-dimensional stable manifold Ws tangent to
Es at
has
k eigenvalues with negative real parts and n-k eigenvalues with positive real parts. Then there exists
k-dimensional stable manifold Ws tangent to
Es at ![]() ,
and n-k-dimensional
unstable manifold Wu tangent to Eu at
,
and n-k-dimensional
unstable manifold Wu tangent to Eu at
![]() ,
such that Ws and Wu
are positively invariant and negatively invariant sets of
(3.14), respectively, and
,
such that Ws and Wu
are positively invariant and negatively invariant sets of
(3.14), respectively, and
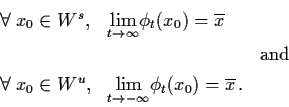

![]() is
given by
is
given by
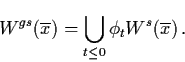
![]() is given by
is given by
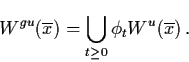
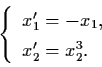
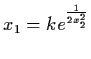 and the
origin is a nonlinear saddle.
and the
origin is a nonlinear saddle.

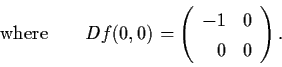
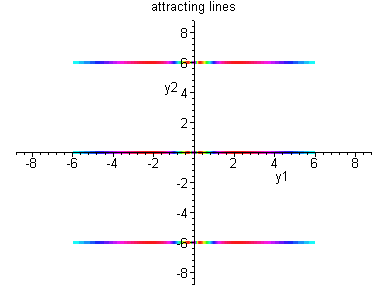
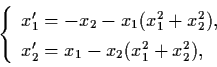

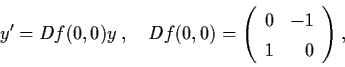

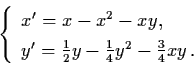
![]() ,
would
give rise to the above equilibrium states.
,
would
give rise to the above equilibrium states.

![\begin{displaymath}A = Df (\ol{x}) = \left[ \begin{array}{cc}
1-2x-y & -x \\
- ...
...rac{3}{4}
x \end{array} \right]_{x=\ol{x} \atop y=\ol{y}} \, .
\end{displaymath}](img570.gif)
![\begin{displaymath}A =\left[ \begin{array}{cc}
1 & 0 \\ 0 & \frac{1}{2} \end{array} \right] \, ,
\lambda_{1} = 1, \lambda_{2} = \frac{1}{2}.
\end{displaymath}](img572.gif)
![]() ,
,
![]() .
.