Next: Hamiltonian systems Up: Nonlinear Systems Previous: The Hartman-Grobman theorem

3.5 Stability of equilibria

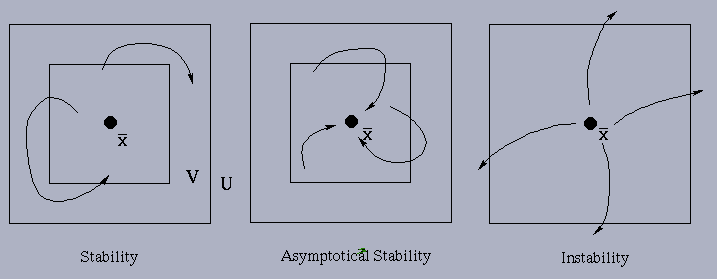
In this section we introduce the important idea of stability of an equilibrium point of a system of ordinary differential equations. An equilibrium point $\ol{x}$ is stable if all nearby solutions stay nearby. It is asymptotically stable if all nearby solutions not only stay nearby, but also tend to $\ol{x}$ .

Consider the nonlinear system

x' = f(x)

(3.19)

we have the following definition.

Definition 3.5.1: Let $\ol{x} \in \Omega$ , $\Omega \subset R^{n}$ , be an equilibrium point of the system (3.19) and $\phi_{t}$ be the flow defined by (3.19). Then $\ol{x}$ is said to be

(i)

stable if $\forall \; \veps > 0, \, \exists \, \delta > 0$ such that

$\begin{displaymath}\mid x_{0} - \ol{x} \mid \, < \, \delta \quad \mbox{implies} ... ... (x_{0}) - \ol{x} \mid \, < \veps \, , \quad t \geq t_{0} \, ; \end{displaymath}$

(ii)

asymptotically stable if (i) holds and moreover there exists $\sigma > 0$ such that

$\begin{displaymath}\mid x_{0} - \ol{x} \mid \, < \, \sigma \quad \mbox{implies} \quad \lim_{t \raro \infty} \phi_{t} (x_{0}) = \ol{x} \, ; \end{displaymath}$

(iii)

unstable if (i) fails to hold.

In 2-d, the above concepts can be described by the following phase diagram:

It follows from Theorems 3.1.1, 3.1.3 and 3.4.1 that the equilibrium point $\ol{x}$ of (3.19) is asymptotically stable if it is a sink, unstable if it is a source or a saddle. In other words, a hyperbolic equilibrium point of (3.19) is either asymptotically stable or unstable. This also implies that stable equilibrium points which are not asymptotically stable can only occur at nonhyperbolic equilibrium points. But the question as to whether a nonhyperbolic equilibrium point is stable, asymptotically stable or unstable is a delicate one.

To motivate a method, which is very useful in answering this question, we discuss a simple example below.

Example 3.5.1: Consider the nonlinear system

$\begin{displaymath}\left\{ \begin{array}{l} x_{1}' = x_{2}, \\ x_{2}' = - x_{1} - x_{1}^{~3} \, . \end{array} \right. \end{displaymath}$

(3.20)

which models the undamped hard spring with x₁ = x and x₂ = x'. System (3.20) has a unique equilibrium point (0,0), which is non-hyperbolic since the matrix
$Df (0,0) = \left[ \begin{array}{rl} 0 & 1 \\ -1 & 0 \end{array} \right]$ has eigenvalues $\lambda = \pm i$ with zero real part. The total energy, i.e. the kinetic energy and the potential energy, of system (3.20) is

$\begin{displaymath}E (x_{1}, x_{2}) = \frac{1}{2} x_{1}^{2} + \frac{1}{4} x_{1}^{4} + \frac{1}{2} x_{2}^{2} \end{displaymath}$

whose derivative along solutions of (3.20) is

$\begin{displaymath}\frac{dE}{dt} = \nabla E (x_{1}, x_{2}) \cdot f (x_{2}, x_{2}... ..._{1}^{~3}) (x_{1} + x_{1}^{3}) (x_{2} , -x_{1} -x_{1}^{3}) = 0 \end{displaymath}$

which expresses conservation of energy.

Thus E(x₁(t), x₂(t)) = E(x₁(0), x₂ (0)), $t \geq 0$ , for any solution of (3.20), i.e.

$\begin{displaymath}\frac{1}{2} x_{1}^{2} (t) + \frac{1}{4} x_{1}^{~4}(t) + \frac... ...4} x_{10}^{4} + \frac{1}{2} x_{20}^{2}\, , \quad t \geq 0 \, , \end{displaymath}$

which implies

$\begin{displaymath}x_{1}^{2} (t) + x_{2}^{2} (t) \leq x_{10}^{2} + \frac{1}{2} x_{10}^{4} + x_{20}^{2} \, , \quad t \geq 0 \, . \end{displaymath}$

Thus $\forall \; \veps \in (0,1)$ , choose $\delta = \frac{\veps}{\sqrt{2}}$ . Then $\sqrt{x_{10}^{2} + x_{20}^{2}} < \delta$ implies

$\begin{displaymath}\mid \phi_{t} (x_{10}, x_{20}) \mid \, \leq \, \sqrt{\frac{3}... ... \cdot \frac{\veps}{\sqrt{2}} < \veps \, , \quad t \geq 0 \, . \end{displaymath}$

Hence by Definition 3.5.2, the equilibrium point (0,0) of (3.19) is stable.

Example 3.5.1 Simulation

The following method, given by A.M. Lyapunov, a Russian mathematician and engineer, in his doctoral thesis in 1892, is a generalization of the (energy) idea contained in the preceding example.

Let $V :\Omega \raro R$ be a C¹ function. Then the derivative of V along solutions of (3.19) is defined as

$\begin{displaymath}\dot{V} (x) = \frac{dV(x(t))}{dt} = \nabla V (x) \cdot f(x) \, . \end{displaymath}$

(3.21)

It follows that the sign of $\nabla V \cdot f$ determines whether V increases or decreases along solutions of (3.19).

Theorem 3.5.1: Let $\ol{x}$ be an equilibrium point of (3.19), $\Omega \subset R^{n}$ be an open set containing $\ol{x}$ , and $V :\Omega \raro R$ be continuously differentiable such that

a): $V (\ol{x}) = 0$ and V(x) > 0 if $x \neq \ol{x}$ .

Then

b)

if $\dot{V} (x) \leq 0$ , $x \in \Omega$ ,

$\ol{x}$ is stable,

c)

if $\dot{V} (x) < 0$ , $x \in \Omega \backslash \{ \ol{x} \}$ ,

$\ol{x}$ is asymptotically stable,

d)

if $\dot{V} (x) > 0$ , $x \in \Omega \backslash \{ \ol{x} \}$ ,

$\ol{x}$ is unstable.

Before proving this theorem, we discuss some examples and try to get some geometric intuition.

Example 3.5.2: Consider the nonlinear system

$\begin{displaymath}\left\{ \begin{array}{l} x' = - y - x^{3} \, , \\ y' = x - y^{3} \, . \end{array} \right. \end{displaymath}$

(3.22)

which has a unique equilibrium, (0,0).

Since $Df(0,0) = \left[ \begin{array}{lr} 0 & -1 \\ 1 & 0 \end{array} \right]$ and $\lambda = \pm i$ , i.e. $Re (\lambda ) = 0$ , it follows that no conclusion can be made by linearization.

To apply the Lyapunov method, we set V (x,y) = x² + y². Then

$\begin{displaymath}\dot{V} (x,y) = \nabla V \cdot f = - 2 (x^{4} + y^{4}) < 0 \quad \mbox{if} \quad (x,y) \neq (0,0) \, . \end{displaymath}$

Also $V(x,y) \geq 0$ and V(x,y) = 0 iff (x,y) = (0,0).

Thus by Theorem 3.5.1, (0,0) is asymptotically stable.

Example 3.5.2 Simulation

Example 3.5.3: Consider the nonlinear system

$\begin{displaymath}\left\{ \begin{array}{l} x' = 2y + x^{5} \\ y' = - x + y^{3} \end{array} \right. \end{displaymath}$

(3.23)

which has a unique equilibrium (0,0), $Df(0,0) = \left[ \begin{array}{rl} 0 & 2 \\ -1 & 0 \end{array} \right]$ , $\lambda = \pm \sqrt{2} i$ . Thus no conclusion can be made by linearization.

But let V(x,y) = x² + 2y². Then V(x,y) > 0 if $(x,y) \neq (0,0)$ , V(0,0) = 0 and $\dot{V} (x,y) = 2x^{6} + 4y^{4} > 0$ if $(x,y) \neq (0,0)$ . Thus by Theorem 3.5.1, (0,0) is unstable.

Example 3.5.3 Simulation

The function V in Theorem 3.5.1 is often called Lyapunov function. It is called positive definite if a) is satisfied, negative definite if -V is positive definite, and ``strict'' Lyapunov function if a) and c) hold.

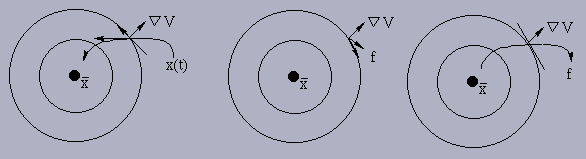
To get an intuitive idea about Theorem 3.5.1, we note that a) implies that $\ol{x}$ is a strict local minimum point of V. Thus we expect the level sets of V, in a neighbourhood of $\ol{x}$ , to be concentric curves (n=2) or surfaces (n=3). Recall that if $\nabla V (a) \neq 0$ , then $\nabla V(a)$ is orthogonal to the level set V(x) - V(a) through a and points outward, and $\nabla V \cdot f = \parallel \nabla V \parallel \; \parallel f \parallel \cos \theta$ , where $\theta$ is the angle between $\nabla V$ and f. Thus if

$\begin{displaymath}\nabla V (x) \cdot f (x) < 0, \quad \mbox{for} \quad x \in \Omega\backslash \{ \ol{x} \} \, , \end{displaymath}$

then V decreases along all orbits in $\Omega\backslash \{ \ol{x} \}$ and any orbit in $\Omega\backslash \{ \ol{x} \}$ will cut the level sets of V inward. We expect that this will continue until the orbit is forced to approach $\ol{x}$ as $t \raro \infty$ , i.e. $\ol{x}$ is asymptotically stable. If we have, instead,

$\begin{displaymath}\nabla V (x) \cdot f (x) \leq 0, \quad \mbox{for} \quad x \in \Omega \backslash - \{ \ol{x} \} \end{displaymath}$

then some orbit in $\Omega\backslash \{ \ol{x} \}$ may stay on the level set V as a periodic solution. In this case, we have stability. Finally, if

$\begin{displaymath}\nabla V (x) \cdot f (x) > 0, \quad \mbox{for} \quad x \in \Omega \backslash \{ \ol{x} \} \, , \end{displaymath}$

then any orbit in $\Omega\backslash \{ \ol{x} \}$ will cut the level sets outward and be forced away from $\ol{x}$ , which yields instability.

Proof of Theorem 3.5.1: (omitted)

The beauty of the Lyapunov function approach lies in the fact that no knowledge of solutions is required. Thus it exhibits great power in applications. It should be noted, that there is no rigid scheme to construct Lyapunov functions, especially, when the systems are written in a general setting. Maybe this is one of the reasons why Lyapunov's stability theory has lasted so long and is still a very active area of research. However, in the case of equations which model physical systems, e.g. mechanical systems, there will be some natural candidates, which can be seen in the next section.

It should be noted that when $\ol{x}$ is a sink of (3.19), one can construct, in view of Theorem 3.1.2, V(x) in a neighbourhood of $\ol{x}$ . Namely V(x) = x^T Qx, where Q is a positive definite matrix and satisfies

$\begin{displaymath}A^{T} Q + QA = - I, \quad A = Df (\ol{x}) \, . \end{displaymath}$

Moreover, V(x) is a ``strict'' Lyapunov function which shows, by Theorem 3.5.1, asymptotic stability of $\ol{x}$ .

You might question why we would even bother to consider the Lyapunov's method when linearization works. The purpose was to really ``tie up loose ends'' and provide a complete picture of the successes and failures of both methods. Again, the ``triumph'' of the Lyapunov's method is to boldly go where linearization could not take us, i.e. eigenvalues with zero real parts. It should be noted that information obtained by linearization can be very misleading in real world problems. The extent of the stability, e.g. the size of the region of attraction and the behaviour of transients as they approach the equilibrium is determined by the nonlinearity of the system. Lyapunov's method takes nonlinearity into account. When one can find Lyapunov functions, they make quantitative information available.

Next: Hamiltonian systems Up: Nonlinear Systems Previous: The Hartman-Grobman theorem