4.3 Poincaré-Bendixson theorem

We discuss, in this section, the existence of periodic solutions. This problem is much more complicated than that of the existence of constant solutions. We only restrict our attention to 2-dimensional systems of the form

$$x' = f(x), \quad x \in R^{2} \, .$$ (4.11)

The higher dimensional systems will be treated in other advanced courses, e.g. AM 751.

Let's start with an example as motivation.

Example 4.3.1:     Consider the nonlinear system

$$\left\{ \begin{array}{l} x_{1}' = x_{2} , \\ x_{2}' = - x_{1... ...1}^{2} - \frac{1}{4} x_{2}^{2}) x_{2} \, . \end{array} \right.$$ (4.12)

Let $V(x_{1}, x_{2}) = \frac{1}{2} (x_{1}^{2} + x_{2}^{2})$. Then

$$\dot{V} (x_{1}, x_{2}) = \left( 1-x_{1}^{2} - \frac{1}{4} x_{2}^{2} \right) x_{2}^{2} \, .$$

By inspection, $\dot{V} (x_{1}, X_{2}) = \frac{3}{4} x_{2}^{4} \geq 0$ on the circle C₁: x₁² + x₂² = 1 and

$$\dot{V} (x_{1}, x_{2}) = - \frac{3}{4} x_{1}^{2} x_{2}^{2} \l... ...ox{on the circle} \quad C_{2} : x_{1}^{2} + x_{2}^{2} = 4 \, .$$

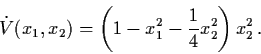
It thus follows that the annulus

$$S = \{ (x_{1}, x_{2}) \in R^{2}; \, 1 \leq x_{1}^{2} + x_{2}^{2} \leq 4 \}$$

is positively invariant. Hence $\forall \; x_{0} \in S$, $\omega (x_{0}) \neq \phi$ and $\omega (x_{0}) \subset S$. Since $\omega (x_{0})$ must be a whole orbit or union of whole orbits and S contains no equilibrium points, it is natural to conjecture that $\omega (x_{0})$ must be a periodic orbit or union of periodic orbits. But the following Lemma shall exclude the possibility that $\omega (x_{0})$ is a union of periodic orbits.

Example 4.3.1 Simulation

Lemma 4.3.1:     Let M be a positively invariant compact set of (4.11). Then for any $x_{0} \in M$, we have

(i)

$\omega (x_{0})$ is closed;

(ii)

$\omega (x_{0})$ is connected.

Proof: (omitted)

Now, we are in a position to state the following Poincaré-Bendixson Theorem.

Theorem 4.3.1:     Let $f \in C^{1} (\Omega )$, $\Omega \subset R^{2}$ is open. Let $x_{0} \in \Omega$ and $\omega (x_{0})$ be a nonempty $\omega$-limit set of (4.11). If

(i)

$\omega (x_{0}) \subset \Omega$ is bounded;

(ii)

$\omega (x_{0})$ contains no equilibrium points;

then $\omega (x_{0})$ is a periodic orbit.

Proof: (omitted)

Remark:     For a more detailed proof, see Perko, p. 226-231 or Hirsch & Smale, p. 242-249.

Corollary 4.3.1:     Let S be a positively invariant compact set of (4.11). Then S contains an equilibrium point or a periodic solution of (4.11).

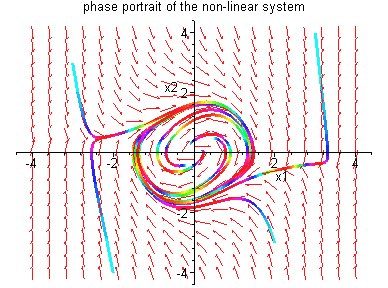
Example 4.3.2:     Consider the nonlinear system

$$\left\{ \begin{array}{l} x_{1}' = 2 x_{2} + (9-4x_{1}^{2} - x_{2}^{2}) x_{1}, \\ x_{2}' = - 3 x_{1} \, . \end{array} \right.$$ (4.13)

Let V(x₁, x₂) = 3 x₁² + 2 x₂². Then $\dot{V} (x_{1}, x_{2}) = 6 x_{1}^{2} (9-4x_{1}^{2} - x_{2}^{2})$. Consider
$S = \left\{ \frac{1}{2} \leq 3 x_{1}^{2} + 2x_{2}^{2} \leq 18 \right\}$. Then we have

$$\begin{array}{lll} \dot{V} (x_{1}, x_{2}) = 6 x_{1}^{2} (8+2x... ...box{on the ellipse} & 3x_{1}^{2} + 2x_{2}^{2} = 18. \end{array}$$

Thus S is a positively invariant set. Since S is compact, it follows from Corollary 4.3.1 that the system (4.13) has at least one periodic solution contained on S.

$\dot{V} = 0$ on the ellipse

$$\frac{x_{1}^{2}}{\frac{9}{4}} + \frac{x_{2}^{2}}{9} = 1 \, .$$

The level curve V = c is the ellipse

$$\frac{x_{1}^{2}}{c/3} + \frac{x_{2}^{2}}{c/2} = 1 \, , \quad c > 0 \, .$$

$$c = \frac{1}{2} \, , \quad \frac{x_{1}^{2}}{\frac{1}{6}} + \frac{x_{2}^{2}}{\frac{1}{4}} = 1,$$

$$c = 18 \, , \quad \frac{x_{1}^{2}}{6} + \frac{x_{2}^{2}}{9} = 1 \, .$$

Example 4.3.2 Simulation

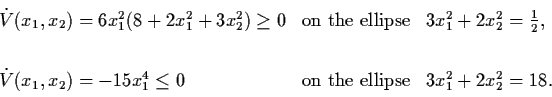
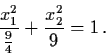
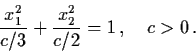
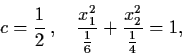
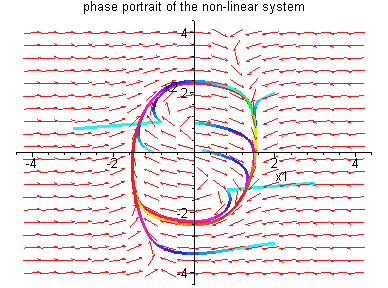
It should be noted that, in both Example 4.3.1 and 4.3.2, the unique equilibrium point (0,0) is enclosed by the periodic solution. This observation turns out to be true in general.

Theorem 4.3.2:     The orbit $\gamma$ of a periodic solution must enclose at least one equilibrium point.

Proof: (omitted)

Corollary 4.3.2:     Let $D \subset R^{2}$ be an open and simply connected set and $f \in C^{1} (\ol{D})$. If D contains no equilibrium points of (4.11), then there is no periodic solutions of (4.11) lying entirely in $\ol{D}$.