| |
(4.14) |
Although the Poincaré-Bendixson theorem can be used to infer the existence of at least one periodic solution, it provides no information on the stability property of the periodic solution. We consider, in this section, some physical systems and establish some stronger results.
The following Van der Pol equation
![\begin{displaymath}\left[ x' +\mu \left( \frac{x^{3}}{3} - x \right) \right]'
+ x = 0 \, .
\end{displaymath}](img925.gif)
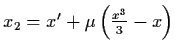 ,
the Van der Pol equation
reduces to
,
the Van der Pol equation
reduces to
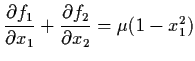 and hence by Theorem 4.2.1, any periodic
orbit must include a portion outside the strip
x12 = 1, as well as a portion inside this strip.
and hence by Theorem 4.2.1, any periodic
orbit must include a portion outside the strip
x12 = 1, as well as a portion inside this strip.
Theorem 4.4.1: There exists a unique isolated
periodic orbit for (4.15) which is asymptotically stable.
Proof: (omitted)
In 1928, a French scientist, Alfred Liénard, was also
interested in self-sustained oscillations and considered a
more general equation
Let
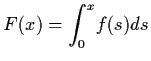 and
and
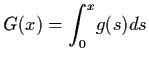 .
Then (4.25) is equivalent to
.
Then (4.25) is equivalent to
Theorem 4.4.2: (Liénard's theorem)
Assume that
Proof: (omitted)
The Liénard's equation has been studied by many mathematicians for the past sixty years and still remains an object of research.
In 1923, Dulac showed that a planar system with f(x) analytic in
![]() cannot have an
infinite number of limit cycles in
cannot have an
infinite number of limit cycles in ![]() provided
provided
![]() is bounded, and if f(x) is a
polynomial system, then (4.14) has at most a finite number
of limit cycles in R2.
is bounded, and if f(x) is a
polynomial system, then (4.14) has at most a finite number
of limit cycles in R2.
Theorem 4.4.3: (Dulac) Let f(x)
be analytic on ![]() .
Then system (4.14) has at most
a finite number of isolated periodic orbits in
.
Then system (4.14) has at most
a finite number of isolated periodic orbits in ![]() if
if ![]() is bounded. If f(x) is a
polynomial, then (4.14) has at most a finite number of
isolated periodic orbits in R2.
is bounded. If f(x) is a
polynomial, then (4.14) has at most a finite number of
isolated periodic orbits in R2.
Errors were recently found in Dulac's original proof and are corrected in 1988, independently, by a group of French mathematicians and the Russian mathematician Y. Ilyashenko.
In 1900, David Hilbert presented a list of 23 mathematical
problems to the 2![]() International Congress of
Mathematicians. The 16
International Congress of
Mathematicians. The 16![]() is the following
question: What is the maximum number of isolated periodic
orbits of an autonomous ODE in R2 if the vector
field f(x) is a polynomial function? This problem
is still unsolved even for the case of quadratic
polynomials. In 1962, the Russian mathematician N.V.
Bautin proved that any quadratic system has at most three
local limit cycles. And it had been believed that the
upper bound was three until in 1979, the Chinese
mathematicians S.L. Shi, L.S. Chen and M.S. Wang produced
examples of quadratic systems with four limit cycles. For
a detailed discussion of this topic, see the monograph
``Theory of limit cycles'' by Yanqian Ye published in 1986.
is the following
question: What is the maximum number of isolated periodic
orbits of an autonomous ODE in R2 if the vector
field f(x) is a polynomial function? This problem
is still unsolved even for the case of quadratic
polynomials. In 1962, the Russian mathematician N.V.
Bautin proved that any quadratic system has at most three
local limit cycles. And it had been believed that the
upper bound was three until in 1979, the Chinese
mathematicians S.L. Shi, L.S. Chen and M.S. Wang produced
examples of quadratic systems with four limit cycles. For
a detailed discussion of this topic, see the monograph
``Theory of limit cycles'' by Yanqian Ye published in 1986.